 which passes through
points
which passes through
points  and
and 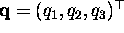 must satisfy
must satisfy



This section describes some basic operations for manipulating points and lines in homogeneous coordinates.
(a) Computing a line through two points. Using Equation
(5), the line  which passes through
points
which passes through
points  and
and 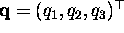 must satisfy
must satisfy


The simplest way to remember the solution to these equations is as a cross-product

(b) Computing the point of concurrency of two lines.
Using Equation (5), the point of concurrency 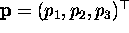 of the
lines
of the
lines 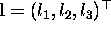 and
and 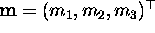 must satisfy
must satisfy


Note how the formulation of this problem mirrors problem (a). This is a
manifestation of the principle of duality -
in any construction or theorem involving points and lines on the
projective plane, each instance of a point
can be exchanged for an instance of a line, and each instance of a
line exchanged for an instance of a point, and the result is a dual
construction or theorem to the original one (in particular this is
useful because for any theorem which is true, its dual is also
true). Thus, this is the dual problem to (b) and is solved in the
same way,
Thus, this is the dual problem to (b) and is solved in the
same way,

Remaining operations in this section are not part of projective geometry. They have been included because they are of practical use.
(c) Normalising homogeneous coordinates. The manipulations of points and lines may result in homogeneous coordinates with very large or very small magnitudes. This can cause numerical error so it is a good idea to normalise homogeneous coordinates at each stage of a computation. Normalisation can be carried out in a straightforward way since a homogeneous vector can be multiplied by any scalar and it will still represent the same point or line. A suggested normalisation for a point is
and for a line
The denominator can be zero in both Equations (12) and (13), in which case any alternative
normalisation which is convenient for the associated application can
be used instead.
The reason for the particular form of the line normalisation is to
produce simple formulae in the operations
in  and
and 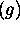 below.
below.
(d) Computing a line through many points.
Computing a line through two points as described in (a) involves the
solution of two equations in two unknowns (although the equations
actually contain three
unknowns a, b, c, it is only the ratios 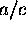 and
and 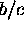 which
are significant because the scale of the homogeneous vector
which
are significant because the scale of the homogeneous vector
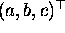 is arbitrary). Given n points, there are n equations in 2
unknowns and the system can be solved using a least-squares method.
is arbitrary). Given n points, there are n equations in 2
unknowns and the system can be solved using a least-squares method.
Two approaches were investigated for this thesis - orthogonal regression and Kanatani's ``moment matrix'' [Kanatani 1992]. In the latter, the computation of different weightings for individual points in the way described by Kanatani was not implemented. These methods produced slightly different results but neither one was consistently better than the other.
(e) Computing the point of concurrency of many lines. This is the dual problem to (d), and is solved in the same way.
(f) Computing the perpendicular distance from a line to a
point. Normalise the line and point as described in (c). If the
line vector is 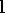 and the point vector is
and the point vector is 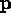 , the
perpendicular distance is given by the dot product
, the
perpendicular distance is given by the dot product
And, when the line and point are incident

Equation (14) has a simple form as a result of the
particular normalisation applied to  and
and  - see
[Faux 1979] for the equation for the general case.
- see
[Faux 1979] for the equation for the general case.
(g) Computing the angle between two lines. Normalise the lines
as described in (c). If
the normalised lines are 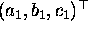 and
and
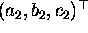 , the angle between them is given by
, the angle between them is given by
Equation (16) has a simple form as a result of the particular normalisation applied to the two lines - see [Faux 1979] for the equation for the general case.


