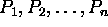 , we
shall write
, we
shall write 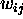 for the weight on the link from
for the weight on the link from 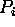 to
to 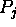 (a weight of 0 implies that there is no such link).
Each processor
(a weight of 0 implies that there is no such link).
Each processor 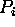 further has an associated
threshold
further has an associated
threshold 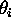




We shall consider simple processors (or units or neurons or perceptrons) which each have an associated activity level 0 or 1.
Processors may be linked to other processors - these links are directed, meaning that a given processor has a number of inputs and a number of outputs. Each of the I/O links has an associated weight, a real number (which may be negative).
If the processors are labelled 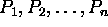 , we
shall write
, we
shall write 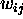 for the weight on the link from
for the weight on the link from 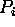 to
to 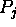 (a weight of 0 implies that there is no such link).
Each processor
(a weight of 0 implies that there is no such link).
Each processor 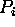 further has an associated
threshold
further has an associated
threshold 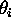
If the current activity level of 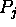 is
is 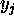 , we define the
total
input
to
, we define the
total
input
to 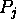 as
as
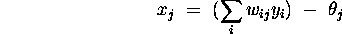
We have the option of introducing a special
bias processor 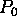 whose activity level
is permanently 1, and which is an input to all other processors.
The weight on the link from this special processor to
whose activity level
is permanently 1, and which is an input to all other processors.
The weight on the link from this special processor to 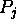 shall be
shall be
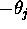 ; we can then write
; we can then write
and assume 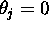 for all j.
for all j.
We determine the activity level of 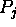 from the value of its input.
We shall write
from the value of its input.
We shall write

The adjustment of the 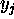 ( firing) is usually taken to be
asynchronous.
( firing) is usually taken to be
asynchronous.
Considering a trivial network formed by just one such processor,
we may use its output as a binary classifier of its n inputs.
Suppose input patterns
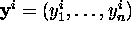 may
belong to class A or B, and we wish the perceptron to output
0 in the former case and 1 in the latter.
For simplicity we introduce the element
may
belong to class A or B, and we wish the perceptron to output
0 in the former case and 1 in the latter.
For simplicity we introduce the element 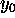 which is
uniformly 1, representing the bias input.
Then if the weights on the perceptron's input lines are
which is
uniformly 1, representing the bias input.
Then if the weights on the perceptron's input lines are
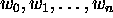 we have the
Perceptron learning algorithm
which iterates the weights
to a configuration which performs the classification we desire.
we have the
Perceptron learning algorithm
which iterates the weights
to a configuration which performs the classification we desire.
Perceptron learning algorithm
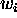 randomly
randomly
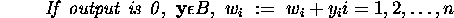
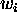 stabilise.
stabilise.
This simple form of the learning algorithm is open to many
amendments/improvements; in particular in equation 2, a
multiplicative constant may be applied to the 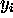 to slow convergence
of the weights, and prevent
`overstepping' of a good solution.
Better, this multiplicative constant can be chosen to suit the quality
of the current weight set, so if the solution is very poor, a
high factor may be chosen, otherwise a small one.
This is the
Widrow-Hoff
learning rule, also called the
Widrow-Hoff delta rule,
or simple the Delta rule.
If, for a given
to slow convergence
of the weights, and prevent
`overstepping' of a good solution.
Better, this multiplicative constant can be chosen to suit the quality
of the current weight set, so if the solution is very poor, a
high factor may be chosen, otherwise a small one.
This is the
Widrow-Hoff
learning rule, also called the
Widrow-Hoff delta rule,
or simple the Delta rule.
If, for a given 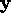 , the desired result is d, set
, the desired result is d, set


Thus the weight change is in proportion to the distance of the weighted sum x (equation 1) from the correct binary decision.
The learning algorithm can be shown to converge satisfactorily, provided a solution exists. This is a result of some power, originally due to Rosenblatt, and is known as the Perceptron convergence theorem.
History
The power of the perceptron was noted by Rosenblatt, who went to elaborate lengths in publicising it. This drew the attention of Minsky, who in early days built mechanical perceptrons that were remarkably successful, demonstrating `damage resistance', learning, and other hitherto unobserved features. Minsky went on to produce a very detailed theoretical analysis of the perceptron which turns out to be limited to linearly separable tasks, and therefore of little practical value. In particular, it is trivial to show that one perceptron cannot perform a parity test on a two bit input. Minsky and Papert's book Perceptrons was a death knell for mainstream work on neural networks, which were not examined again until the pioneering work of Rumelhart, McClelland et al. in the mid 80's (this last point is a romantic misrepresentation of the truth, which does great disservice to a number of distinguished workers in the field).



