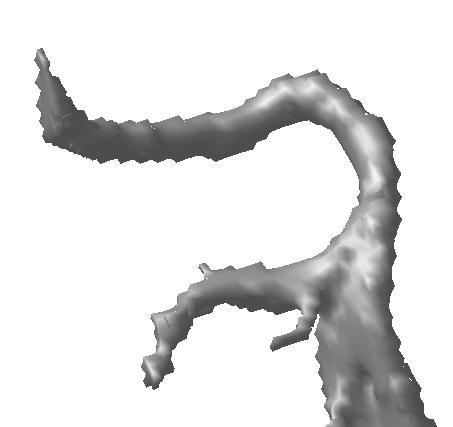
Divergence-Based Medial Surfaces
Sylvain Bouix & Kaleem Siddiqi
McGill University
School of Computer Science &
Center for Intelligent Machines
3480 University Street
Montreal, QC H3A 2A7, Canada
{sbouix,siddiqi}@cim.mcgill.ca
Introduction
Medial surface based representations are of significant interest for a number of
applications in biomedicine, including object representation
[15,25], registration [12] and
segmentation [20]. Such descriptions are also popular for
animating objects in graphics [26,18] and manipulating them
in computer-aided design. They provide a compact representation while preserving
the object's genus and retain sufficient local information to reconstruct (a
close approximation to) it. This facilitates a number of important tasks
including the quantification of the local width of a complex structure, e.g.,
the grey matter in the human brain, and the analysis of its topology, e.g., the
branching pattern of blood vessels in angiography images. Graph-based
abstractions of such data have also been proposed [7]. Despite
their popularity, the stable numerical computation of medial surfaces remains a
challenging problem. Unfortunately, the classical difficulties associated with
computing their 2D analog, the Blum skeleton, are only exacerbated when a third
dimension is added.
Background
The 2D skeleton of a closed set
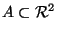 is the locus of centers of
maximal open discs contained within the complement of the set [5]. An
open disc is maximal if there exists no other open disc contained in the
complement of A that properly contains the disc.
is the locus of centers of
maximal open discs contained within the complement of the set [5]. An
open disc is maximal if there exists no other open disc contained in the
complement of A that properly contains the disc.
The medial surface of a closed set
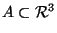 is
defined in an analogous fashion as the locus of centers of maximal
open spheres contained in the complement of the set. It is often
referred to as the 3D skeleton, though this term is misleading since
it is in fact comprised of a collection of 3D points, curves and
surfaces [3].
is
defined in an analogous fashion as the locus of centers of maximal
open spheres contained in the complement of the set. It is often
referred to as the 3D skeleton, though this term is misleading since
it is in fact comprised of a collection of 3D points, curves and
surfaces [3].
Whereas the above definition is quite general, in the current context
we shall assume that the closed set A is the bounding surface of a
volumetric object. Hence, this set will have two complementary medial
surfaces, one inside the volume and the other outside it. In most
cases we shall be referring to the former, though the development
applies to both.
Interest in the medial surface as a representation for a volumetric object stems
from a number of useful properties:
- 1.
- it is a thin set, i.e., it contains no interior points
- 2.
- it is homotopic to the volume,
- 3.
- it is invariant under Euclidean transformations of the volume (rotations and
translations)
- 4.
- given the radius of the maximal inscribed sphere associated which each medial surface point, the volumetric object can be reconstructed exactly.
Hence, it provides a compact representation while
preserving the object's genus and making certain properties explicit,
such as its local width.
The following figure illustrate the medial surface of a cube.
A cube
|
|

|

|
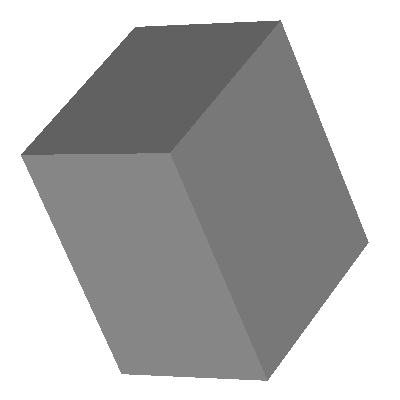
|
its medial surface
|

|

|

|
Thinning
Approaches to computing skeletons and medial surfaces can be broadly organized
into three classes. First, methods based on thinning attempt to realize Blum's
grassfire formulation [5] by peeling away layers from an object, while
retaining special points [2,10,14]. It is
possible to define erosion rules in a lattice such that the topology
of the object is preserved. However, these methods are quite sensitive to
Euclidean transformations of the data and typically fail to localize skeletal or
medial surface points accurately. As a consequence, only a coarse approximation
to the object is usually reconstructed [14,4,10].
Voronoi skeletons
Second, it has been shown that under appropriate smoothness
conditions, the vertices of the Voronoi diagram of a set of boundary
points converges to the exact skeleton as the sampling rate
increases [19]. This property has been exploited to
develop skeletonization algorithms in 2D [16], as well
as extensions to 3D [21,22]. The dual of the
Voronoi diagram, the Delaunay triangulation (or tetrahedralization in
3D) has also been used extensively. Here the skeleton is defined as
the locus of centers of the circumscribed spheres of each tetraheda
[8,15]. Both types of methods preserve topology and
accurately localize skeletal or medial surface points, provided that
the boundary is sampled densely. Unfortunately, however, the
techniques used to prune faces and edges which correspond to small
perturbations of the boundary are typically based on heuristics. In
practice, the results are not invariant under Euclidean
transformations and the optimization step, particularly in 3D, can
have a high computational complexity [15].
Distance functions
A third class of methods exploits the fact that the locus of skeletal or medial
surface points coincides with the singularities of a Euclidean distance
function to the boundary. These approaches attempt to detect local maxima of
the distance function, or the corresponding discontinuities in its
derivatives [1,11,9]. The numerical
detection of these singularities is itself a non-trivial problem; whereas it may
be possible to localize them, ensuring homotopy with the
original object is difficult.
Divergence-based skeletons
In recent work we observed that the grassfire flow leads to a
hamilton-jacobi equation, which by nature is conservative in the
smooth regime of its underlying phase
space [24]. Hence, we suggested that a
measurement of the net outward flux per unit volume of the gradient
vector field of the Euclidean distance function could be used to
associate locations where a conservation of energy principle was
violated with medial surface
points [23]. Unfortunately, in practice, the
resulting medial surface was not guaranteed to preserve the topology
of the object, since the flux computation was a purely local
operation. The main contribution of the current paper is the
combination of the flux measurement with a homotopy preserving
thinning process applied in a cubic lattice. The method is robust and
accurate, has low computational complexity and is now guaranteed to
preserve topology. There are other promising recent approaches which
combine aspects of thinning, Voronoi diagrams and distance
functions [13,28,6,27]. In spirit, our
method is closest to that of [13]
1 but is grounded in
principles from physics.
For more details about this method please refer to the papers presented at ICCV'99 and ECCV'00
Examples
We illustrate the algorithm with volumes
segmented from MR and MRA images. In these simulations we have used
the D-Euclidean distance transform, which provides a close
approximation to the true Euclidean distance.
A brain ventricle
|

|
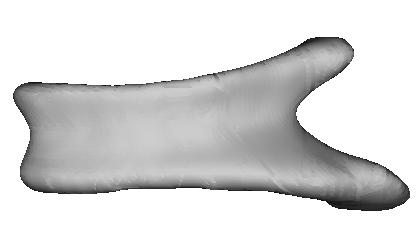
|
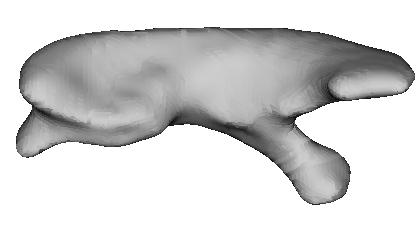
|
its medial surface
|

|

|
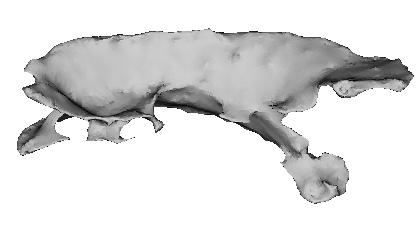
|
We are grateful to Allen Tannenbaum and Steve Zucker for
collaborations on the hamilton-jacobi formulation. Louis Collins,
Georges Le Goualher, Belinda Lee and Terry Peters kindly supplied the
medical data. This research was supported by CFI, FCAR and NSERC.
- 1
-
C. Arcelli and G. S. di Baja.
Ridge points in euclidean distance maps.
Pattern Recognition Letters, 13(4):237-243, 1992.
- 2
-
C. Arcelli and G. Sanniti di Baja.
A width-independent fast thinning algorithm.
IEEE PAMI, 7(4):463-474, July 1985.
- 3
-
V. I. Arnold.
Mathematical Methods of Classical Mechanics.
Springer-Verlag, 1989.
- 4
-
G. Bertrand.
A parallel thinning algorithm for medial surfaces.
Pattern Recognition Letters, 16:979-986, 1995.
- 5
-
H. Blum.
Biological shape and visual science.
Journal of Theoretical Biology, 38:205-287, 1973.
- 6
-
G. Borgefors, I. Nystrom, and G. S. D. Baja.
Computing skeletons in three dimensions.
Pattern Recognition, 32:1225-1236, 1999.
- 7
-
E. Bullitt, S. Aylward, A. Liu, J. Stone, S. K. Mukherjee, C. Coffey, G. Gerig,
and S. M. Pizer.
3d graph description of the intracerebral vasculature from segmented
mra and tests of accuracy by comparison with x-ray angiograms.
In IPMI'99, pages 308-321, 1999.
- 8
-
J. A. Goldak, X. Yu, and A. K. abd Lingxian Dong.
Constructing discrete medial axis of 3-d objects.
Int. Journal of Computational Geometry and Applications,
1(3):327-339, 1991.
- 9
-
J. Gomez and O. Faugeras.
Reconciling distance functions and level sets.
Technical Report TR3666, INRIA, April 1999.
- 10
-
T.-C. Lee and R. L. Kashyap.
Building skeleton models via 3-d medial surface/axis thinning
algorithm.
CVGIP: Graphical Models and Image Processing, 56(6):462-478,
November 1994.
- 11
-
F. Leymarie and M. D. Levine.
Simulating the grassfire transform using an active contour model.
IEEE PAMI, 14(1):56-75, jan 1992.
- 12
-
A. Liu, E. Bullitt, and S. M. Pizer.
3d/2d registration via skeletal near projective invariance in tubular
objects.
In MICCAI'98, pages 952-963, 1998.
- 13
-
G. Malandain and S. Fernandez-Vidal.
Euclidean skeletons.
Image and Vision Computing, 16:317-327, 1998.
- 14
-
A. Manzanera, T. M. Bernard, F. Preteux, and B. Longuet.
Medial faces from a concise 3d thinning algorithm.
In ICCV'99, pages 337-343, Kerkyra, Greece, September 1999.
- 15
-
M. Näf, O. Kübler, R. Kikinis, M. E. Shenton, and G. Székely.
Characterization and recognition of 3d organ shape in medical image
analysis using skeletonization.
In IEEE Workshop on Mathematical Methods in Biomedical Image
Analysis, 1996.
- 16
-
R. Ogniewicz.
Discrete Voronoi Skeletons.
Hartung-Gorre, 1993.
- 17
-
L. Perko.
Differential Equations and Dynamical Systems.
Springer-Verlag, 1986.
- 18
-
S. M. Pizer, A. Thall, and D. T. Chen.
M-reps: A new object representation for graphics.
ACM Transactions on Graphics (submitted), 1999.
- 19
-
M. Schmitt.
Some examples of algorithms analysis in computational geometry by
means of mathematical morphology techniques.
In J. Boissonnat and J. Laumond, editors, Lecture Notes in
Computer Science, Geometry and Robotics, volume 391, pages 225-246.
Springer-Verlag, 1989.
- 20
-
T. B. Sebastian, H. Tek, J. J. Crisco, S. W. Wolfe, and B. B. Kimia.
Segmentation of carpal bones from 3d ct images using skeletally
coupled deformable models.
In MICCAI'98, pages 1184-1194, 1998.
- 21
-
D. J. Sheehy, C. G. Armstrong, and D. J. Robinson.
Shape description by medial surface construction.
IEEE Transactions on Visualization and Computer Graphics,
2(1):62-72, 1996.
- 22
-
E. C. Sherbrooke, N. Patrikalakis, and E. Brisson.
An algorithm for the medial axis transform of 3d polyhedral solids.
IEEE Transactions on Visualization and Computer Graphics,
2(1):44-61, 1996.
- 23
-
K. Siddiqi, S. Bouix, A. Tannenbaum, and S. W. Zucker.
The hamilton-jacobi skeleton.
In ICCV'99, pages 828-834, Kerkyra, Greece, September 1999.
- 24
-
K. Siddiqi, A. Tannenbaum, and S. W. Zucker.
A hamiltonian approach to the eikonal equation.
In EMMCVPR'99, pages 1-13, York, UK, July 1999.
- 25
-
G. D. Stetten and S. M. Pizer.
Automated identification and measurement of objects via populations
of medial primitives, with application to real time 3d echocardiography.
In IPMI'99, pages 84-97, 1999.
- 26
-
M. Teichmann and S. Teller.
Assisted articulation of closed polygonal models.
In 9th Eurographics Workshop on Animation and Simulation, 1998.
- 27
-
H. Tek and B. B. Kimia.
Symmetry maps of free-form curve segments via wave propagation.
In ICCV'99, pages 362-369, Kerkyra, Greece, September 1999.
- 28
-
Y. Zhou, A. Kaufman, and A. W. Toga.
3d skeleton and centerline generation based on an approximate minimum
distance field.
Int. Journal of the Visual Computer, 14(7):303-314, 1998.
Footnotes
- ...[13]
1
- Malandain and Fernandez-Vidal use a heuristic estimation of
the singularities of a distance function to obtain an initial skeleton
or medial surface, and then perform a topological reconstruction to
ensure homotopy with the original shape.
Sylvain Bouix and Kaleem Siddiqi
2000-10-23

![]() is
defined in an analogous fashion as the locus of centers of maximal
open spheres contained in the complement of the set. It is often
referred to as the 3D skeleton, though this term is misleading since
it is in fact comprised of a collection of 3D points, curves and
surfaces [3].
is
defined in an analogous fashion as the locus of centers of maximal
open spheres contained in the complement of the set. It is often
referred to as the 3D skeleton, though this term is misleading since
it is in fact comprised of a collection of 3D points, curves and
surfaces [3].