Our goal is to recover the depth ![]() and the curvature kt at
P. It has been shown that these values are related to the position and the curvature of the
epipolar curves. Therefore, the problem is to
estimate two of these curves given three tangents.
The previous section showed that the epipolar curves are, up to
order 2, parabolas of the epipolar planes. Moreover, although the
epipolar curves are not in the same plane, by using proposition 2,
linear estimations of both
and the curvature kt at
P. It has been shown that these values are related to the position and the curvature of the
epipolar curves. Therefore, the problem is to
estimate two of these curves given three tangents.
The previous section showed that the epipolar curves are, up to
order 2, parabolas of the epipolar planes. Moreover, although the
epipolar curves are not in the same plane, by using proposition 2,
linear estimations of both ![]() and kt can be derived.
and kt can be derived.
Now consider the epipolar plane ![]() . We denote by
. We denote by ![]() the angle between the normal N at P and its projection
the angle between the normal N at P and its projection
![]() in
in ![]() :
:
![]()
![]()
Since P1 belongs to the epipolar curve, the tangent to ![]() at P1
in the direction T1 goes through the point
at P1
in the direction T1 goes through the point ![]() and
it follows that:
and
it follows that:
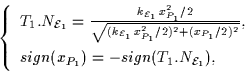
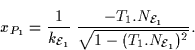
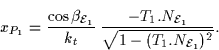 |
(7) |
T1, ![]() and
and ![]() can be computed from image measurements.
Thus, we can determine the distance
can be computed from image measurements.
Thus, we can determine the distance ![]() between
the intersection of the tangents and P given the curvature kt. In
addition, it was
shown (section 2.2) that the distance between the camera
centre C and the intersection of the tangents can also be computed from image
measurements. Hence, if this distance is denoted by d1, we have the
following relation:
between
the intersection of the tangents and P given the curvature kt. In
addition, it was
shown (section 2.2) that the distance between the camera
centre C and the intersection of the tangents can also be computed from image
measurements. Hence, if this distance is denoted by d1, we have the
following relation:
| |
(8) |
Likewise, since T is also tangent to the second epipolar curve in
the epipolar plane ![]() , the depth at P can also be
computed in the plane
, the depth at P can also be
computed in the plane ![]() . Hence, by (8) and (9):
. Hence, by (8) and (9):
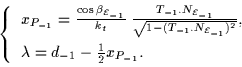
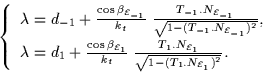 |
(9) |
Remark The connection with the depth formula (3) as written in 2.2 becomes clear if we write (see figure 8):
![]()
![]()
![]()
The special case ![]() or equivalently
or equivalently
![]() occurs when the normal N at P is orthogonal to
the epipolar plane. This implies that P is a multiple
point and thus
occurs when the normal N at P is orthogonal to
the epipolar plane. This implies that P is a multiple
point and thus ![]() . However, if the camera motion is not along the line of
sight at P (
. However, if the camera motion is not along the line of
sight at P (![]() ), the depth at such points can still
be computed since in this case two or more different image projections of P are available. This points out that d-1 and d1 should be computed
using a robust formula instead of
), the depth at such points can still
be computed since in this case two or more different image projections of P are available. This points out that d-1 and d1 should be computed
using a robust formula instead of ![]() which is not defined at a multiple point (i.e.
which is not defined at a multiple point (i.e. ![]() ). See the appendix for details on how we compute
). See the appendix for details on how we compute ![]() .
.
Finally, by solving (10) and assuming that camera motions are not along any line of sight, we obtain the following solutions:
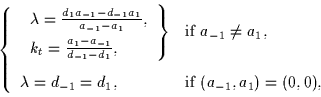 |
(10) |
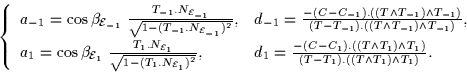
A geometrical interpretation of d1 and d-1 is that they represent the distances from the camera centre position C to the viewing line intersections (see 2.2). To give an interpretation of the terms a1 and a-1, consider the projection of P1 and P-1 onto the viewing line at P. Intuitively, a1 and a-1) can be seen as the positions of these projected points with respect to P. Hence, if P is a double point, then either a1 or a-1 is null and if P is a triple point, then both a1 and a-1 are null.
Remark The above solutions are not defined if a-1 =
a1 and ![]() . This corresponds to
situations where the projections of P-1 and P1 onto
the viewing line at P are the same. Thus, the contributions of the
viewing directions T-1 and T1 in
(10) are equal and the system has an infinity of
solutions. However, unique solutions for depth and the normal curvature kt
at such points P can still be found. The idea is to first compute the
depth at one of the epipolar correspondents P1 or P-1. This
can be done by applying (10) at p1 (or
equivalently p-1). To this aim, two epipolar correspondents to
p1 (or equivalently p-1) must be found. We already have p
and we can also use p-1 (or equivalently p1) since
p-1 and p1 are epipolar
correspondents in that particular case. Once the depth at P1 has been
computed, we can determine the depth at P by the fact that they both
belong to the same parabola. Then, the equation given by applying
(10) at P gives the normal curvature kt.
. This corresponds to
situations where the projections of P-1 and P1 onto
the viewing line at P are the same. Thus, the contributions of the
viewing directions T-1 and T1 in
(10) are equal and the system has an infinity of
solutions. However, unique solutions for depth and the normal curvature kt
at such points P can still be found. The idea is to first compute the
depth at one of the epipolar correspondents P1 or P-1. This
can be done by applying (10) at p1 (or
equivalently p-1). To this aim, two epipolar correspondents to
p1 (or equivalently p-1) must be found. We already have p
and we can also use p-1 (or equivalently p1) since
p-1 and p1 are epipolar
correspondents in that particular case. Once the depth at P1 has been
computed, we can determine the depth at P by the fact that they both
belong to the same parabola. Then, the equation given by applying
(10) at P gives the normal curvature kt.![]()
We conclude that the position of a rim point and the normal curvature kt in the viewing direction can be estimated at any regular point and double point, except if the camera motion is in the viewing direction. For points where more than two rims intersect (i.e., (a-1,a1) = (0,0)) and with the same exception, depth can be estimated but not the normal curvature. And if the camera motion is along one of the viewing directions T-1 or T1, neither curvatures nor the depth at P can be computed.