Why three occluding contours are needed to recover depth along the view line

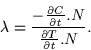
Our goal is to recover rims from their projections. First, we suppose that under a continuous motion of the camera a complete description of the spatio-temporal surface is available. Then, (1) can be derived according to time t and by taking the scalar product with the normal N to the surface, we obtain:  

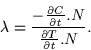$$\lambda = \frac{-\frac{\partial C}{\partial t}.N}{\frac{\partial T}{\partial t}.N}.$$ (2)

This is the depth formula for points on rims as defined in [Cip 90]. Assuming that we have a parametrisation of ${\cal S}$, we can therefore compute $\frac{\partial T}{\partial t}$ from the spatio-temporal surface and then recover the depth for points on the spatio-temporal surface where $\frac{\partial T}{\partial t}.N \neq 0$. Unfortunately, only discrete information (occluding contours at discrete times $t_i, i \in [1..m]$) are available and (2) can not be applied directly. In fact, depth can be computed only by approximation. In this section, we discuss such an approximation.

Now consider two successive occluding contours at times t₁ and t₂. Let P₁ and P₂ be two points on the rims of ${\cal S}$ at t₁ and t₂. Using the notations of the previous section, we have:

$$\left\{ \begin{array} {ll} r_1= C_1+\lambda_1 T_1 & \mbox{at... ...},\ r_2=C_2 +\lambda_2 T_2& \mbox{at $P_2$}.\end{array}\right.$$

Thus, denoting by $\Delta x$the difference $\Delta x = x_1 - x_2$, where x is any of r, C, $\lambda$ and T, gives:

$$\Delta r = \Delta C + \lambda_1\, \Delta T +\Delta \lambda\, T_2,$$

and by taking the scalar product with the normal N₂ to the surface at P₂, we obtain the following depth formula for point P₁:

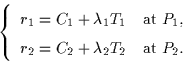
If the image projections p₁ and p₂ of P₁ and P₂ are matched according to the epipolar correspondence, then the first term of the above expression corresponds to a triangulation formula. Indeed, $\frac{-\Delta C.N_2}{\Delta T.N_2}$ is the distance from the camera centre C₁ to the viewlines intersection (see figure 6). This value is therefore the depth of a virtual point with image projection p₁ and p₂. Hence, it can be computed from measurements in two images by using a stereo formula.

  

Figure 6: Intersection of tangents in the epipolar plane.

On the other hand, the second term of (3) depends on the distance $\Delta r$ between surface points P₁ and P₂. This value can not be computed, a priori, from measurements in two images. A first approach would consist in omitting this term in (3). We could then recover the depth of a surface point with only two images. But this approach leads to a stereo reconstruction and implicitly assumes that rims are not view dependent which is of course wrong. For a smooth surface which is not locally plane, $\Delta r.N_2\neq 0$ except at a multiple point. Therefore, the second term of (3) should not be omitted when computing depth.

The approach we have developed is based on a local surface model: a second order approximation. Such a model allows $\Delta r.N_2$ to be expressed as a function of local properties of ${\cal S}$. Hence, by using more than two images (three for a second order approximation), we can fit locally the surface model to the image measurements and estimate both depth and local properties. This idea is developed in the next section.