The proposed two-pass algorithm defines a corner in a simple
and intuitively appealing way, as a location where a triangle of specified size
and opening angle can be inscribed in a curve.
A curve is represented by a sequence of points ![]() in the image plane.
The ordered points are densely sampled along the curve, but, contrary
to the other four algorithms, no regular spacing between them is assumed.
A chain-coded curve can also be handled if converted to a sequence of grid points.
In the first pass the algorithm scans the sequence and selects candidate
corner points. The second pass is post-processing to remove superfluous
candidates.
in the image plane.
The ordered points are densely sampled along the curve, but, contrary
to the other four algorithms, no regular spacing between them is assumed.
A chain-coded curve can also be handled if converted to a sequence of grid points.
In the first pass the algorithm scans the sequence and selects candidate
corner points. The second pass is post-processing to remove superfluous
candidates.
First pass. In each curve point ![]() the detector tries to inscribe
in the curve a variable triangle
the detector tries to inscribe
in the curve a variable triangle
![]() constrained by a set of simple rules:
constrained by a set of simple rules:
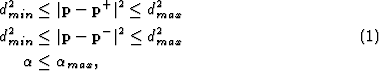
where
![]() is the distance between
is the distance between ![]() and
and ![]() ,
,
![]() the distance between
the distance between ![]() and
and ![]() , and
, and
![]() the opening angle of the triangle.
(See figure 1a.) The latter is computed as
the opening angle of the triangle.
(See figure 1a.) The latter is computed as
![\begin{figure}
\begin{center}
\subfigure[]{\illustr{/corner/corner1.eps}{0.42}}...
...ad
\subfigure[]{\illustr{/corner/corner2.eps}{0.38}}
\end{center} \end{figure}](img65.gif) |
Variations of the triangle that satisfy the conditions (7)
are called admissible. Search for the admissible variations starts from ![]() outwards and stops if any of the conditions (7) is violated.
(That is, a limited number of neighboring points is only considered.)
Among the admissible variations, the least
opening angle
outwards and stops if any of the conditions (7) is violated.
(That is, a limited number of neighboring points is only considered.)
Among the admissible variations, the least
opening angle
![]() is selected.
is selected.
![]() is assigned
to
is assigned
to ![]() as the sharpness of the candidate.
If no admissible triangle can be inscribed,
as the sharpness of the candidate.
If no admissible triangle can be inscribed, ![]() is
rejected and no sharpness is assigned.
is
rejected and no sharpness is assigned.
Considering the vector product of
![]() and
and
![]() ,
it is easy to see
that the corner is convex if
,
it is easy to see
that the corner is convex if
![]() ,
otherwise it is concave.
,
otherwise it is concave.
Second pass. The sharpness based non-maxima suppression procedure is illustrated in figure 1b. A corner detector can respond to the same corner in a few consecutive points. Similarly to edge detection, a post-processing step is needed to select the strongest response by discarding the non-maxima points.
A candidate point ![]() is discarded
if it has a sharper valid neighbor
is discarded
if it has a sharper valid neighbor ![]() :
:
![]() .
In the current implementation,
a candidate point
.
In the current implementation,
a candidate point ![]() is a valid neighbor of
is a valid neighbor of ![]() if
if
![]() .
As alternative definitions, one can use
.
As alternative definitions, one can use
![]() or the points adjacent to
or the points adjacent to ![]() .
.
Parameters. ![]() ,
,
![]() and
and
![]() are the
parameters of the algorithm.
are the
parameters of the algorithm.
![]() sets the scale (resolution), with small values responding to
fine corners. The upper limit
sets the scale (resolution), with small values responding to
fine corners. The upper limit ![]() is necessary to avoid false sharp
triangles formed by distant points in highly varying curves.
is necessary to avoid false sharp
triangles formed by distant points in highly varying curves.
![]() is the angle limit that determines the minimum sharpness
accepted as high curvature. In practice, we often set
is the angle limit that determines the minimum sharpness
accepted as high curvature. In practice, we often set
![]() and tune the remaining two parameters,
and tune the remaining two parameters, ![]() and
and
![]() .
The default values are
.
The default values are ![]() and
and
![]() .
.