, the 
distribution of the parameters can be approximated by a quadratic form (Taylor series expansion):
Assuming the errors have a Gaussian distribution, the inverse Hessian matrix of a chi-square distribution of function parameters, sufficiently close to the minimum, is the estimated covariance matrix of standard errors of these parameters.
If we are close enough to the minimum, , the distribution of the parameters can be approximated by a quadratic form (Taylor series expansion):
as there is no gradient at the minimum, the second term will disappear.
The gradient of the Chi-square distribution wrt to an element of 
is:
Taking another partial derivative:
As 
is a random measurement error that can have either sign, summing over them will cause the second term will disappear.
Now the Hessian is:
Once we have the value for H, we can invert it and use it as an estimate of the error covariance of the parameters.
By using the gradient of each datapoint wrt to each parameter, we can use error propagation (see appendix A) to estimate the errors:
The diagonal elements of this covariance matrix give the probable error at each datapoint.
We put this method to the test for fitting a polynomial 
with a data measurement accuracy (standard error) of 0.08 on each element. Figure 4 shows a comparison of the predicted error on each datapoint against the true error (averaged over 1000 fits), as found by a least-squares fit. The script error_estimation.m demonstrates this.
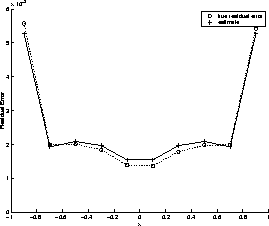
Figure 4: Error prediction on 
with an error of 
on each point