Next: Distribution-Based Many-to-Many Matching
Up: Metric Embedding of Graphs
Previous: Construction of Spherical Codes
Encoding Directed Edges
The distance metric defined on the graph structure is based on the
undirected edge weights. While the above embedding has preserved the
distance metric, it has failed to preserve any oriented relations,
such as the hierarchical relations common to scale-space structures.
This is due to the fact that oriented relations do not satisfy the
symmetry property of a metric. We can retain this important
information in our embedding by moving it into the nodes as node
attributes, a technique used in the encoding of directed topological
structure in [20], directed geometric structure in
[19], and shape context in [2]. Encoding in a node
the attributes of the oriented edges incident to the node requires
computing distributions on the attributes and assigning them to the
node. For example, a node with a single parent at a coarser scale and
two children at a finer scale might encode a relative scale
distribution (histogram) as a node attribute. The resulting attribute
provides a contextual signature for the node which will be used by the
matcher (Section 5) to reduce matching
ambiguity.
Specifically, let
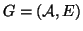 be a graph to be embedded. For every
pair of vertices,
be a graph to be embedded. For every
pair of vertices, 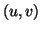 , we let
, we let 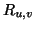 denote the attribute vector
associated with the pair. The entries of each such vector
represent the set of oriented relations
denote the attribute vector
associated with the pair. The entries of each such vector
represent the set of oriented relations 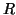 between
between 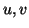 . For a
vertex
. For a
vertex
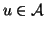 , we let
, we let 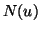 denote the set of vertices
denote the set of vertices
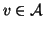 adjacent to
adjacent to 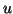 . For a relation
. For a relation 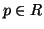 , we will denote
, we will denote
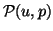 as the set of values for relation
as the set of values for relation 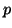 between
between 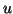 and all
vertices in
and all
vertices in 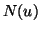 , i.e.,
, i.e., 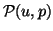 corresponds to entry
corresponds to entry 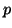 of
vector
of
vector 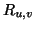 for
for 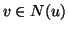 . Feature vector
. Feature vector 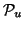 for
point
for
point 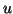 is the set of all
is the set of all 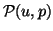 's for
's for 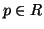 . Observe
that every entry
. Observe
that every entry 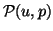 of vector
of vector 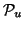 can be
considered as a local distribution (histogram) of feature
can be
considered as a local distribution (histogram) of feature 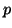 in
the neighborhood
in
the neighborhood 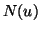 of
of 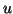 . We adopt the method of
[19], in which the distance function for two such vectors
. We adopt the method of
[19], in which the distance function for two such vectors
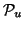 and
and 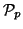 is computed through a weighted
combination of Hausdorff distances between
is computed through a weighted
combination of Hausdorff distances between 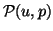 and
and
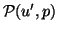 for all values of
for all values of 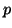 .
.
Next: Distribution-Based Many-to-Many Matching
Up: Metric Embedding of Graphs
Previous: Construction of Spherical Codes