Next: Encoding Directed Edges
Up: Metric Embedding of Graphs
Previous: Construction of a Tree
Construction of Spherical Codes
To embed our metric trees into Euclidean spaces of fixed dimension, we
introduce the concept of spherical codes. Such codes, in turn,
will allow us to directly compare two embeddings. The embedding
framework is best illustrated through an example, in which a weighted
tree is embedded into
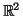 , as shown in
Figure 4. To ease visualization, we will limit
the discussion to the first quadrant. The weighted tree contains 4
paths
, as shown in
Figure 4. To ease visualization, we will limit
the discussion to the first quadrant. The weighted tree contains 4
paths
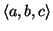 ,
,
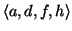 ,
,
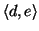 , and
, and
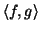 in its caterpillar decomposition. In the embedding, the root
is assigned to the origin. Next, we seek a set of
in its caterpillar decomposition. In the embedding, the root
is assigned to the origin. Next, we seek a set of  vectors, one for
each path in the caterpillar decomposition, such that their inner
products are minimized, i.e., their endpoints are maximally apart.
These vectors define the general directions in which the vertices on
each path in the caterpillar decomposition will be embedded.
vectors, one for
each path in the caterpillar decomposition, such that their inner
products are minimized, i.e., their endpoints are maximally apart.
These vectors define the general directions in which the vertices on
each path in the caterpillar decomposition will be embedded.
Figure 4:
An edge weighted tree and its spherical code in 2D. The Cartesian
coordinates of the vertices are: 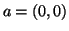 ,
, 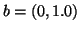 ,
,
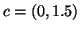 ,
, 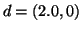 ,
, 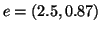 ,
, 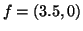 ,
, 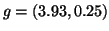 ,
and
,
and 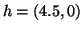 .
.
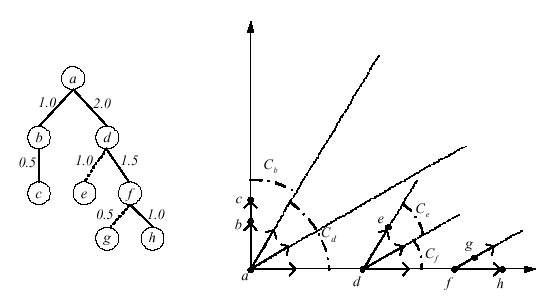 |
Three of the four vectors will be used by the caterpillar paths
belonging to the subtree rooted at vertex 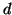 , and one vector will be
used by the path belonging to the subtree rooted at vertex
, and one vector will be
used by the path belonging to the subtree rooted at vertex 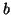 . This
effectively subdivides the first quadrant into two cones,
. This
effectively subdivides the first quadrant into two cones, 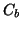 and
and
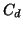 . The volume of these cones is a function of the number of
caterpillar paths belonging to the subtrees rooted at
. The volume of these cones is a function of the number of
caterpillar paths belonging to the subtrees rooted at 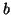 and
and 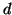 . The
cone
. The
cone 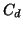 , in turn, will be divided into two smaller cones,
, in turn, will be divided into two smaller cones, 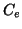 and
and
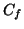 , corresponding to the subtrees rooted at
, corresponding to the subtrees rooted at 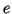 and
and 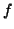 ,
respectively. The extreme rays of sub-cones
,
respectively. The extreme rays of sub-cones 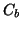 ,
, 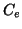 , and
, and 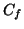 will correspond to the 4 directions defining the embedding. Finally,
to complete the embedding, we translate the sub-cones away from the
origin along their directional rays to positions defined by the path
lengths in the tree. For example, to embed point
will correspond to the 4 directions defining the embedding. Finally,
to complete the embedding, we translate the sub-cones away from the
origin along their directional rays to positions defined by the path
lengths in the tree. For example, to embed point 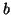 , we will move
along the extremal ray of
, we will move
along the extremal ray of 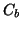 and will embed
and will embed 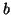 at
at 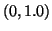 .
Similarly, the sub-cone
.
Similarly, the sub-cone 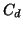 will be translated along the other
extremal ray, embedding
will be translated along the other
extremal ray, embedding 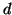 at
at 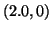 .
In
.
In 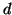 -dimensional Euclidean space
-dimensional Euclidean space
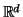 , computing the embedding
, computing the embedding
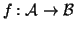 under
under 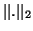 is more involved. Let
is more involved. Let 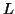 denote
the number of paths in the caterpillar decomposition. The embedding
procedure defines
denote
the number of paths in the caterpillar decomposition. The embedding
procedure defines 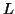 vectors in
vectors in
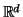 that have a large angle with
respect to each other on the surface of a hypersphere
that have a large angle with
respect to each other on the surface of a hypersphere 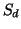 of radius
of radius
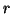 . These vectors are chosen in such a way that any two of their
endpoints on the surface
. These vectors are chosen in such a way that any two of their
endpoints on the surface 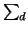 are at least spherical distance 2
from each other. We will refer to such vectors as
well-separated. Consider the set of hyperplanes
are at least spherical distance 2
from each other. We will refer to such vectors as
well-separated. Consider the set of hyperplanes
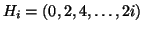 , and let
, and let
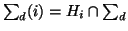 . Since each of
the
. Since each of
the 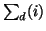 are hypercircles, i.e., surfaces of spheres in
dimension
are hypercircles, i.e., surfaces of spheres in
dimension 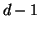 , we can recursively construct well-separated vectors
on each hypercircle
, we can recursively construct well-separated vectors
on each hypercircle 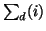 . Our construction stops when the sphere
becomes a circle and the surface becomes a point in 2 dimensions. It
is known that taking
. Our construction stops when the sphere
becomes a circle and the surface becomes a point in 2 dimensions. It
is known that taking 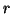 to be
to be
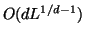 , and the minimum
angle between two vectors to be
, and the minimum
angle between two vectors to be 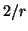 provides us with
provides us with 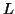 well-separated vectors [6]. In
Figure 4, we have 4 such vectors emanating from
the origin.
Now that the embedding directions have been established, we can
proceed with the embedding of the vertices. The embedding procedure
starts from the root (always embedded at the origin) and embeds
vertices following the embedding of their parents. For each vertex in
the metric tree
well-separated vectors [6]. In
Figure 4, we have 4 such vectors emanating from
the origin.
Now that the embedding directions have been established, we can
proceed with the embedding of the vertices. The embedding procedure
starts from the root (always embedded at the origin) and embeds
vertices following the embedding of their parents. For each vertex in
the metric tree
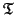 , we associate with every subtree
, we associate with every subtree
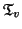 a set
of vectors
a set
of vectors 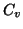 , such that the number of vectors in
, such that the number of vectors in 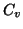 equals the
number of paths in the caterpillar decomposition of
equals the
number of paths in the caterpillar decomposition of
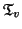 . Initially, the root has the entire set of
. Initially, the root has the entire set of 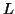 vectors.
Consider a subtree rooted at vertex
vectors.
Consider a subtree rooted at vertex 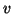 , and let us assume that vertex
, and let us assume that vertex
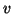 has
has 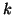 children,
children,
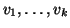 . We partition the set of
vectors into
. We partition the set of
vectors into 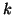 subsets, such that the number of vectors in each
subset,
subsets, such that the number of vectors in each
subset, 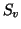 , equals the number of leaves in
, equals the number of leaves in
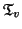 . We then embed
the vertex
. We then embed
the vertex 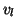 (
(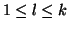 ) at the position
) at the position
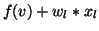 ,
where
,
where 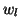 is the length of the edge
is the length of the edge 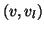 and
and 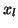 is some
vector in
is some
vector in 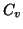 . We recursively repeat the same process for each
subtree rooted at every child of
. We recursively repeat the same process for each
subtree rooted at every child of 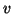 , and stop when there are no more
subtrees to consider.
, and stop when there are no more
subtrees to consider.
Next: Encoding Directed Edges
Up: Metric Embedding of Graphs
Previous: Construction of a Tree

