


Next: Conclusion
Up: Experiments and results
Previous: Description
First, projective displacements 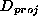 are calculated from point correspondences and epipolar geometry with the method described in [HC98]. Then, the equation of the plane at infinity is calculated and the infinite homographies
are calculated from point correspondences and epipolar geometry with the method described in [HC98]. Then, the equation of the plane at infinity is calculated and the infinite homographies 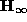 associated to the left camera are derived. Our affine calibration algorithms are similar to [BZ95] and [HC98] and cope with general and planar motions (in this case, we need at least 2 motions). Finally, the real Jordan decomposition of each
associated to the left camera are derived. Our affine calibration algorithms are similar to [BZ95] and [HC98] and cope with general and planar motions (in this case, we need at least 2 motions). Finally, the real Jordan decomposition of each 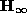 is calculated and the resolution of eq:kkt enables us to obtain the complete camera calibration.
is calculated and the resolution of eq:kkt enables us to obtain the complete camera calibration.
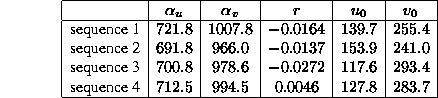
We show the results on 4 motion sequences (each consisting of 5 motions) :
sequence 1 : non singular general motions
sequence 2 : non singular planar motions
sequence 3 : planar motion with a horizontal rotation axis
sequence 4 : planar motion with a vertical rotation axis
The following table exhibits the matrices 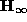 and
and  obtained for the first motion of each sequence. It confirms the particular forms of
obtained for the first motion of each sequence. It confirms the particular forms of 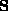 obtained for critical motions.
obtained for critical motions.
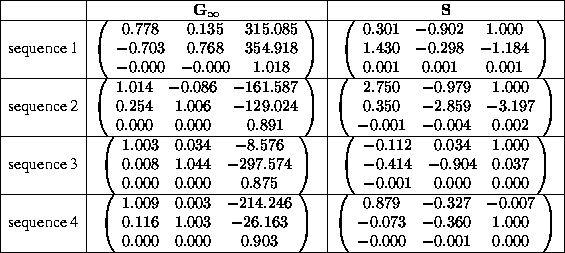
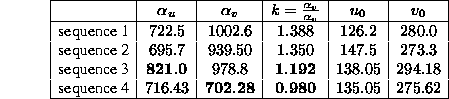
The results of the computation of 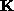 from the previous matrices
from the previous matrices 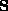 are as follows :
are as follows :
with the assumption r=0, only the first two sequences allow us to calculate 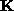 :
:
the assumption 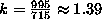 allows us to calculate
allows us to calculate 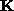 in all sequences :
in all sequences :
From these experiments, we can see clearly that the k-constraint allows us to calibrate even in the case of critical motions. With the r-constraint, we can see that significant errors are made in 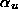 for sequence 3, and in
for sequence 3, and in 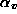 for sequence 4.
for sequence 4.
Bob Fisher
Mon Dec 7 13:48:06 GMT 1998
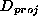 are calculated from point correspondences and epipolar geometry with the method described in [HC98]. Then, the equation of the plane at infinity is calculated and the infinite homographies
are calculated from point correspondences and epipolar geometry with the method described in [HC98]. Then, the equation of the plane at infinity is calculated and the infinite homographies 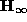 associated to the left camera are derived. Our affine calibration algorithms are similar to [BZ95] and [HC98] and cope with general and planar motions (in this case, we need at least 2 motions). Finally, the real Jordan decomposition of each
associated to the left camera are derived. Our affine calibration algorithms are similar to [BZ95] and [HC98] and cope with general and planar motions (in this case, we need at least 2 motions). Finally, the real Jordan decomposition of each 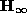 is calculated and the resolution of eq:kkt enables us to obtain the complete camera calibration.
is calculated and the resolution of eq:kkt enables us to obtain the complete camera calibration.


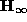 and
and  obtained for the first motion of each sequence. It confirms the particular forms of
obtained for the first motion of each sequence. It confirms the particular forms of  obtained for critical motions.
obtained for critical motions.

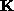 from the previous matrices
from the previous matrices 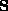 are as follows :
are as follows :
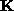 :
:

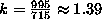 allows us to calculate
allows us to calculate 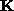 in all sequences :
in all sequences :

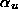 for sequence 3, and in
for sequence 3, and in 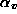 for sequence 4.
for sequence 4.