


Next: References
Up: Autocalibration in the presence
Previous: Results
We have described a method for solving the problem of affine-to-Euclidean calibration, based on the real Jordan decomposition of 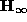 . This allows us to express the ambiguity in the computation of the absolute conic (and also, the intrinsic parameters) as a 1-parameter family.
Although this ambiguity can be solved when many motions with non parallel rotation axes are used, it can not when motions are planar or when we dispose of a single motion. In these cases, we showed that an assumption should be made on one of the internal parameters r or k.
. This allows us to express the ambiguity in the computation of the absolute conic (and also, the intrinsic parameters) as a 1-parameter family.
Although this ambiguity can be solved when many motions with non parallel rotation axes are used, it can not when motions are planar or when we dispose of a single motion. In these cases, we showed that an assumption should be made on one of the internal parameters r or k.
Besides, we showed the existence of 3 classes of critical motion. We saw that r and k didn't have the same role in the resolution of the equations : in particular, the knowledge of k allows us to cope with 2 of the 3 critical motions.
Experiments on noisy synthetic data confirmed the theoretical results and proved it was possible to calibrate a camera in some of the special cases. Experiments we have made on real data (not shown) seem to confirm that in general resolution of the equations with the k-constraint is relatively stable even when the rotation axis is near to the horizontal or vertical axes of the camera.
However, the analysis we made here is only qualitative : we studied which parameters could be obtained for each kind of critical motion. We are currently studying more quantitative extensions to this work which try to analyze the precision and stability of the parameter computation as a function of the motion.
Bob Fisher
Mon Dec 7 13:48:06 GMT 1998
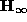 . This allows us to express the ambiguity in the computation of the absolute conic (and also, the intrinsic parameters) as a 1-parameter family.
Although this ambiguity can be solved when many motions with non parallel rotation axes are used, it can not when motions are planar or when we dispose of a single motion. In these cases, we showed that an assumption should be made on one of the internal parameters r or k.
. This allows us to express the ambiguity in the computation of the absolute conic (and also, the intrinsic parameters) as a 1-parameter family.
Although this ambiguity can be solved when many motions with non parallel rotation axes are used, it can not when motions are planar or when we dispose of a single motion. In these cases, we showed that an assumption should be made on one of the internal parameters r or k.


