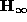 between the images taken with a camera to calibrate, before and after the rigid motion. Once this infinite homography is obtained, it is possible to recover
between the images taken with a camera to calibrate, before and after the rigid motion. Once this infinite homography is obtained, it is possible to recover 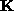 thanks to the relation :
eq:ginf
= -1
thanks to the relation :
eq:ginf
= -1



The affine calibration enables to calculate the infinite homography 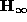 between the images taken with a camera to calibrate, before and after the rigid motion. Once this infinite homography is obtained, it is possible to recover
between the images taken with a camera to calibrate, before and after the rigid motion. Once this infinite homography is obtained, it is possible to recover 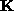 thanks to the relation :
eq:ginf
= -1
thanks to the relation :
eq:ginf
= -1
where 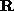 is the rotation of the motion (the Euclidean frame is chosen to be the camera frame). A classical way to solve this equation was first proposed by R.Hartley [Har94] and consists to solve the equation :
is the rotation of the motion (the Euclidean frame is chosen to be the camera frame). A classical way to solve this equation was first proposed by R.Hartley [Har94] and consists to solve the equation :
eq:hartley =
where 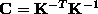 is the image of the absolute conic.
is the image of the absolute conic. 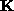 is then obtained by Cholesky decomposition of
is then obtained by Cholesky decomposition of 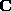 . It is well known that the solutions
. It is well known that the solutions 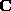 of eq:hartley define a 1-parameter family. This ambiguity can be eliminated if at least 2 motions with non parallel rotation axes are considered.
of eq:hartley define a 1-parameter family. This ambiguity can be eliminated if at least 2 motions with non parallel rotation axes are considered.
We propose another way to solve eq:ginf with an analysis which allows us to identify critical motions and to partially solve for calibration in these particular cases. This analysis is based on the real Jordan decomposition which has already been studied in [CDRH98] in the case of projective displacements. The approach takes into account the fact that eq:ginf defines  as the conjugate of a rotation
as the conjugate of a rotation 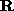 . In an appropriate frame,
. In an appropriate frame, 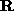 can be reduced to the simple form
can be reduced to the simple form 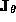 :
:
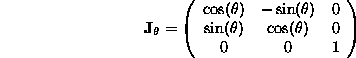
Then, there exists a  matrix
matrix  such that :
eq:decomp
such that :
eq:decomp 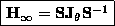
This is a real Jordan decomposition of 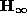 .
.