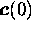 corresponds to
the active ray element
corresponds to
the active ray element 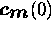 .
Then the relation
.
Then the relation



It can be easily seen that the same contour can be represented both
with active contours and active rays. Without any loss of generality
we assume that the active contour element 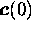 corresponds to
the active ray element
corresponds to
the active ray element 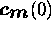 .
Then the relation
.
Then the relation
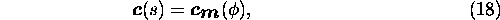
is valid, with the variable substitution 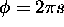 .
.
In the previous section we have looked for an energy term describing some kind of smoothness of a contour. The internal energy of an active contour has been proven to be a good energy description. Thus, we will take exactly this energy term, but substituting the contour representation of snakes by this of active rays. We then get for the internal energy,
Now substituting (9) in (19) we get
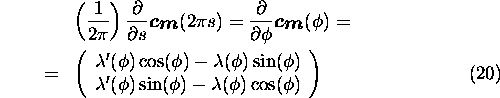
with  .
Similary, we get
.
Similary, we get
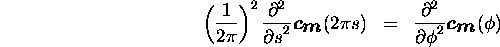
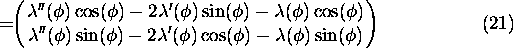
with 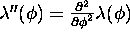 .
Now one can directly compute
.
Now one can directly compute
and
and we get for the internal energy
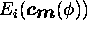 of the active ray
of the active ray
One can see two distance terms in this energy term. Thus, during an energy minimization small distances to the reference point are preferred. This is exactly the behavior of active contours, which shrink to one point in the case of missing external energy. This is not easy to see by the energy description for active contours. In contrast to this, the energy description of active rays makes this behavior obvious. Using exactly the energy term (25) active rays will show the same abilities as active contours, with the exception, that all 2D optimization steps are reduced to 1D. We have already noted, that the shrinking behavior of active contours is not advantageous. Thus, if we neglect the distance term in the internal energy we fix this problem. Additionally it can be shown, that the mixed term does not influence the solution of the Euler--Lagrange differential equation. So, this term can also neglected. As a result one gets the term for the internal energy, as already proposed in equation (10).
=


