


Next: Evolutionary structure recovery
Up: Applying knowledge to reverse
Previous: Inference of unobservables
Euclidean distance is better and fast
One important issue in surface shape fitting and reconstruction
is the choice of error metrics.
For many years, the algebraic metric has been the choice for
fitting quadric surfaces (e.g. [4]).
If
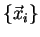 is a set of 3D data points, then the
algebraic fit [22]
is the
is a set of 3D data points, then the
algebraic fit [22]
is the 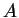 ,
, 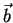 and
and 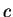 that minimizes
that minimizes
By the appropriate reorganization of the terms of this function,
the minimization can be expressed as an eigenvalue problem with
a straightforward, efficient and numerically stable solution.
In the case of linear structures like planes and lines, this
approach also gives the solution that minimizes the Euclidean
distance to the data.
Unfortunately, there is significant shape bias when fitting
curved surfaces. Taubin's distance and other variants
[52,53,7,58,28]
or shape specific methods [31] are improvements
and can be implemented efficiently, but still with bias.
However, the Euclidean distance is usually the best:
where
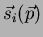 is the point on the fitted surface
(which is parameterized by shape and position parameters
is the point on the fitted surface
(which is parameterized by shape and position parameters 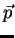 )
closest to data point
)
closest to data point 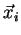 .
Figure 11 shows a comparison of fittings to a real
cylindrical dataset. For this important industrial shape, both
the algebraic and Taubin fitting give serious errors in the fitting,
while the Euclidean fit is good.
.
Figure 11 shows a comparison of fittings to a real
cylindrical dataset. For this important industrial shape, both
the algebraic and Taubin fitting give serious errors in the fitting,
while the Euclidean fit is good.
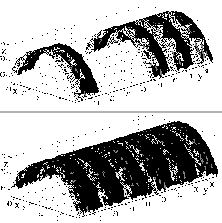
Figure 10:
Cylinder before and after shape and texture restoration
from behind an occlusion.
 |
Researchers and engineers have traditionally avoided using the
Euclidean distance because there is no closed form solution for general
quadric surfaces thus leading to a large computational cost.
(Closed forms exist for planes, elliptical
cylinders and cones, which are a very practical subset of the
quadric surfaces.)
Recently we have reinvestigated this question because of the
recent dramatic increase in computational power [17,16].
As well as exposing the great difference in fit quality, we have
investigated the computational costs.
Our efficient iterative implementation of the Euclidean fit is
about 20 times slower than the closed form Taubin fit, but, in fact, the
actual running time is approaching negligibility.
Our implementation runs at about 3000 points/second on a 500 Mhz PC.
This implies that better quality surface fitting is now possible at
reasonable costs.



Next: Evolutionary structure recovery
Up: Applying knowledge to reverse
Previous: Inference of unobservables
Bob Fisher
2003-08-18
![]() is a set of 3D data points, then the
algebraic fit [22]
is the
is a set of 3D data points, then the
algebraic fit [22]
is the ![]() ,
, ![]() and
and ![]() that minimizes
that minimizes