Summary of the algorithm

The process of rectification can be summarised as follows:

• Given a stereo pair of images I1,I2 and PPMs Po1,Po2 (obtained by calibration);
• compute [T1,T2,Pn1,Pn2] = rectify(Po1,Po2) (see box);
• rectify images by applying T1 and T2.

Reconstruction can be performed from the rectified images directly, using Pn1,Pn2.

   function [T1,T2,Pn1,Pn2] = rectify(Po1,Po2)
   % RECTIFY compute  rectification  matrices  
   %
   % [T1,T2,Pn1,Pn2] = rectify(Po1,Po2) computes the
   % rectifying projection matrices "Pn1", "Pn2", and
   % the rectifying transformation of the retinal plane 
   % "T1", "T2" (in homogeneous coordinate). The arguments  
   % are the  two old projection matrices "Po1" and "Po2".

   % focal lenght
   % (extp(a,b) is external product of vectors a,b)
   au = norm(extp(Po1(1,1:3)', Po1(3,1:3)'));
   av = norm(extp(Po1(2,1:3)', Po1(3,1:3)'));

   % optical centres
   c1 = - inv(Po1(:,1:3))*Po1(:,4);
   c2 = - inv(Po2(:,1:3))*Po2(:,4);

   % retinal planes 
   fl = Po1(3,1:3)';
   fr = Po2(3,1:3)';

   nn = extp(fl,fr);

   % solve the four systems
   A = [ [c1' 1]' [c2' 1]' [nn'  0]' ]';
   [U,S,V] = svd(A);
   r = 1/(norm(V([1 2 3],4)));
   a3 = r * V(:,4);
   A = [ [c1' 1]' [c2' 1]' [a3(1:3)' 0]' ]';
   [U,S,V] = svd(A);
   r = norm(av)/(norm(V([1 2 3],4)));
   a2 = r * V(:,4);
   A = [ [c1' 1]' [a2(1:3)' 0]' [a3(1:3)' 0]' ]';
   [U,S,V] = svd(A);
   r = norm(au)/(norm(V([1 2 3],4)));
   a1 = r * V(:,4);
   A = [ [c2' 1]' [a2(1:3)' 0]' [a3(1:3)' 0]' ]';
   [U,S,V] = svd(A);
   r = norm(au)/(norm(V([1 2 3],4)));
   b1 = r * V(:,4);

   % adjustment
   H = [
     1 0 0 
     0 1 0
     0 0 1 ];

   % rectifying  projection matrices
   Pn1 = H * [ a1 a2 a3 ]';
   Pn2 = H * [ b1 a2 a3 ]';

   % rectifying image transformation
   T1 = Pn1(1:3,1:3)* inv(Po1(1:3,1:3));
   T2 = Pn2(1:3,1:3)* inv(Po2(1:3,1:3));

Notice that, owing to a sign ambiguity in the computation of eigenvalues, the rectified images can experience a reflection along the vertical or horizontal axis. This can be detected by checking whether or not the ordering between the two diagonal corners of the image is preserved. If a reflection occurs, it can be trivially compensated by pre-multiplying both rectifying PPM by a matrix of the form:

with .

Figure 5 is another example of rectification of a generic stereo pair.

  
Figure 5: Top row: a stereo pair (Copyright SYNTIM-INRIA). Bottom row: the rectified pair. The right pictures plot the epipolar lines corresponding to the point marked in the left pictures. Full size images.

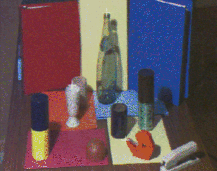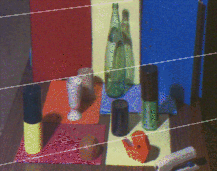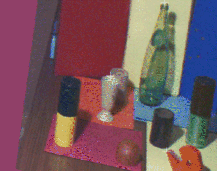The MATLAB code of function rectify and the implementation in C of the image rectification algorithm can be found on line.