2. Mathematical Morphology (Serra,
1982)
Mathematical morphology is
based on geometry. The theoretical foundations of morphological image
processing lies in set theory and the mathematical theory of order. The basic
idea is to probe an image with a template shape, which is called structuring
element, to quantify the manner in which the structuring element fits within a
given image.
2.1 Binary morphology
A
binary image A in the N-dimensional Euclidean space EN can be considered as a
subset of EN: A I EN. The image foreground (set
A) consists of all points zIEN having value 1 and the
image background (set AC) consists of all points zIEN having zero value.
The translation of A by a point x is denoted by A+x or (A)x and is defined as follows:
![]() (1)
(1)
Geometrically, A+x results
by translating every point of A along the vector x. Figure 1 illustrates A+x
and B+x, where A, B I E2. Notice that if a point y
of the input image A coincides with the origin, then this point in the translated
image A+x corresponds to point x.
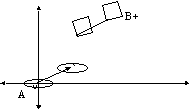
Figure 1. Translations of disk A and square B by x (A, B I E2). Notice that the centre of the disk which coincides with the origin, after the translation by x corresponds to point x.
The reflection of A is denoted by –A or As and is defined as
follows:
![]() (2)
(2)
Figure 2 illustrates -A, where A I E2.
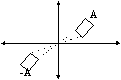
Figure 2. Reflection of rectangular A (AIE2).
Erosion
The fundamental operation of
mathematical morphology is erosion. All mathematical morphology depends on this
notion. The erosion of an input image A by a structuring element B, is defined
as follows:
![]() (3)
(3)
This means that in order to
perform the erosion of A by B we translate B by x so that this lies inside A.
The set of all points x satisfying this condition constitutes ![]() . Figure 3
illustrates the erosion of a triangle by a disk.
. Figure 3
illustrates the erosion of a triangle by a disk.
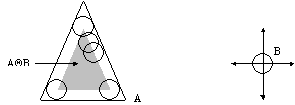
Figure 3. ![]() is the internal triangle, according to eqn (3).
is the internal triangle, according to eqn (3).
The erosion of an image can also be found by intersecting all translates of the input image by the reflection of the structuring element:
![]() (4)
(4)
An example of performing
erosion using eqn (4) is illustrated in Figure 4, (A, B I E2). The arrows denote the origin and the shaded area
represents the set points.

Figure 4. ![]() results from
results from ![]() (the intersection of
some translations of A), according to eqn (4).
(the intersection of
some translations of A), according to eqn (4).
Dilation
The dual operation to erosion is dilation. Dilation of an input image A
by a structuring element B, is defined as follows:
![]() (5)
(5)
This means that
in order to perform the dilation of A by B we first translate B by all points
of A. The union of these translations constitutes ![]() . Figure 5 illustrates the dilation of a triangle by a disk.
. Figure 5 illustrates the dilation of a triangle by a disk.

Figure 5. ![]() is the external triangle with rounded
corners, according to eqn (5).
is the external triangle with rounded
corners, according to eqn (5).
Dilation is both commutative and associative:
![]() and
and ![]() (6)
(6)
By commutativity: ![]() (7)
(7)
This means that dilation can
also be formed by translating the input image by all points in the structuring
element and then taking the union. An application of eqn (7) is illustrated in
the example of Figure 6, (A, B![]() E2).
E2).

Figure 6. ![]() results from
results from ![]() ,
according to eqn (7).
,
according to eqn (7).
Basic Properties of Erosion and Dilation
(i) If the origin lies inside the
structuring element, erosion is anti-extensive
(shrinks the input image)
![]() (8)
(8)
and dilation is extensive (expands the input image)
![]()
![]() (9)
(9)
(ii) Both erosion and
dilation are translation invariant relative
to the input image:
![]() and
and ![]() (10)
(10)
Since dilation is commutative, it is translation invariant relative to
the structuring element. On the other hand erosion is not:
![]() but
but ![]() (11)
(11)
(iii) Both erosion and
dilation are monotonically increasing relative
to a specific structuring element:
![]() and
and ![]() (12)
(12)
Since dilation is commutative, it is monotonically increasing relative to a specific input image, but erosion is not:
![]() but
but ![]() (13)
(13)
(iv) Erosion is dual to dilation
(it is defined via dilation by set complementation) and vice versa:
![]() or
or ![]() (14)
(14)
Thus, eroding an image can be accomplished by dilating the complement of the image, while dilating an image can be accomplished by eroding the complement of the image. In other words, dilation expands the image foreground and shrinks its background, whilst erosion shrinks the image foreground and expands its background.
Opening
A secondary operation of
great importance in mathematical morphology is the opening operation. Opening of an input image A by a structuring
element B is defined as follows:
![]() (15)
(15)
An equivalent definition for opening is:
![]() (16)
(16)
This means that in order to
open A by B we first translate B by x so that this lies inside A. The union of
these translations constitutes ![]() . For instance, the
opening of a triangle A by a disk B (the origin coincides with the centre of
the disk) is the triangle A with rounded corners. In general, opening by a disk
rounds or eliminates all peaks extending into the image background.
. For instance, the
opening of a triangle A by a disk B (the origin coincides with the centre of
the disk) is the triangle A with rounded corners. In general, opening by a disk
rounds or eliminates all peaks extending into the image background.
If ![]() , then A is invariant under opening by B and it is called B-open.
, then A is invariant under opening by B and it is called B-open.
Closing
The other important
secondary operation is closing.
Closing of an input image A by a structuring element B is defined as follows:
![]() (17)
(17)
For instance, closing a
triangle A by a disk B (the origin is on the centre of the disk) yields the
same triangle A. In this case ![]() and we say that A is B-close.
In general, closing by a disk rounds or eliminates all cavities extending into
the image foreground.
and we say that A is B-close.
In general, closing by a disk rounds or eliminates all cavities extending into
the image foreground.
Basic Properties of Opening and Closing
(i) Opening is anti-extensive and
closing is extensive:
![]() and
and ![]() (18)
(18)
(ii) Both opening and
closing are translation invariant:
![]() and
and ![]() (19)
(19)
(iii) Both opening and
closing are monotonically increasing:
![]() and
and ![]() (20)
(20)
(iv) Opening and closing are
is dual operations:
![]() and
and ![]() (21)
(21)
(v) Both opening and closing
are idempotent:
![]() and
and ![]() (22)
(22)
The importance of idempotency is that once an image has been opened (closed), successive openings (closings) do not alter the result (Haralick, et al., 1987). Idempotent transformations are of particular significance since they correspond to the ideal non-realisable band-pass filters of conventional linear filtering; once an image is ideally band-pass filtered, further filtering does not alter the result.
Open-Close Filters
(Dougherty and Astola,
1994)
Suppose that ![]() is an image A
corrupted by pepper noise N (i.e.
granules of noise on the image background). If the corrupted image is opened by
a suitable structuring element B, pepper noise is reduced or totally
eliminated. It can be proven that:
is an image A
corrupted by pepper noise N (i.e.
granules of noise on the image background). If the corrupted image is opened by
a suitable structuring element B, pepper noise is reduced or totally
eliminated. It can be proven that:
![]() (23)
(23)
If A is B-open ![]() , the previous relation becomes:
, the previous relation becomes:
![]() (24)
(24)
It is obvious from relations
(23) and (24) that an ideal structuring element B has the proper shape
and size, so that it completely restores the original image A; i.e. it
eliminates the granules of pepper noise and it permits the whole image A to
pass through the filter. If N is salt
type noise (i.e. holes on the image foreground), we can reduce or eliminate
this noise and restore the original image A by closing the corrupted image by a
proper structuring element B.
Aiming at reducing or
eliminating both, salt and pepper noise, we can first open the corrupted image
by a proper structuring element B and then close the resulting image by the
same structuring element. In this way we implement an open-close filter. In this case, the structuring element must be
not only large enough to eliminate the noise granules but also small enough to
fit between salt holes. If the structuring element does not fit between two
salt holes, during opening the erosion by B will create larger holes, thus
degrading the image foreground. If such a structuring element cannot be chosen,
we can first use an open-close filter with a very small size structuring
element, followed by an open-close filter with a larger size structuring
element, which is followed by an open-close filter with an even larger size
structuring element etc. In this way we implement an alternating sequential filter, which gradually eliminates noise
components from smallest to largest.
2.2 Grey-scale morphology
A grey-scale image A in the
N-dimensional Euclidean space is represented in an N+1-dimensional orthogonal
system (N axes for spatial co-ordinates and one for grey-levels). For signals
N=1 and for images N=2.
Let ![]() at any point z outside the signal (image) frame. We
define:
at any point z outside the signal (image) frame. We
define:
Finite Domain of f(z):![]() (25)
(25)
Spatial translation of f by x: ![]() (26)
(26)
Vertical translation of f by y
(offset): ![]() (27)
(27)
Translation of f in the plane ( f is a signal): ![]() (28)
(28)
Reflection of g through the origin of spatial
co-ordinates axes: g(-z)
(29)
Erosion
The erosion of f
by a structuring element g at
a point x is defined as follows:
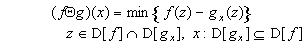 (30)
(30)
This means that we translate
spatially g by x (so that its origin is located at point x) and then we find the minimum of all differences of values of f with the corresponding values of the
translated g, ![]() .
.
An equivalent definition of erosion is:
![]() (31)
(31)
Here we translate f by -x
instead of translating g by x. The example of Figure 7 illustrates
how we use eqns (30) and (31) to perform (fÈg)(x),
(N=2).
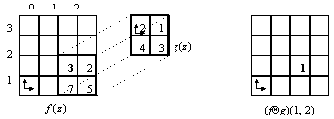
Figure 7. f(1,2)=3, x=(1,2), z = {(0,0),(0,1),(-1,0),(-1,1)}
and ![]()
Indeed, according to eqns (30) and (31) : ![]()
![]()
![]()
![]()
![]()
Dilation
The dilation of f by a structuring element g at a point x is defined as follows:
![]() (32)
(32)
This means that we translate
spatially the reflection of g, g (-z),
so that its origin is located at point x and
then we find the maximum of all sums of values of f with the corresponding values of the translated reflection of g, ![]() .
.
An equivalent definition of dilation is:
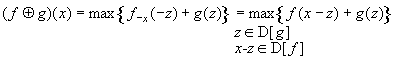 (33)
(33)
An example of performing dilation using eqns (32) and (33) is illustrated in Figure 8. Grey-scale erosion, dilation, opening and closing possess the properties of binary erosion, dilation, opening and closing, respectively.
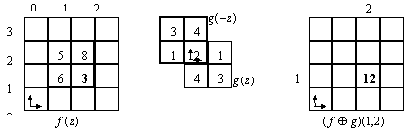
Figure 8. f(1,2)=3 , x=(1,2) , z= {(0,0),(0,1),(-1,0),(-1,1) and
Indeed, according to eqns (32) and (33) : ![]()
![]()
![]()
![]()
![]()
REFERENCES
G. Matheron (1975): Random
Sets and Integral Geometry, Wiley, New York.
J.
Serra (1982): Image Analysis and
Mathematical Morphology, Academic Press, London.
R.
C. Gonzalez and R. E. Woods (1992): Digital
Image Processing, Addison-Wesley, New York.
R.
M. Haralick and L. G. Shapiro (1992): Computer
and Robot Vision, Addison-Wesley, New York.
H. J.
A. M. Heijmans (1994): Morphological
Image Operators, Academic Press, New York.