Estimating local variance for Gaussian filtering

Giovani Gomez
Dept. of Computing
ITESM - Campus Morelos
gegomez@campus.mor.itesm.mx

Abstract:

We present an adaptive Gaussian filter that estimates directly the local amount of Gaussian smoothing in terms of variance. Local variance is selected in a scale-space framework, through the minimal description length criterion (MDL). The MDL allows us to estimate the optimal local smoothing in such a way that it respects the main discontinuities. Experiments show that the adaptive Gaussian filter is very competitive to anisotropic diffusion or a chain of $sigma $-filters. Moreover, the proposed estimation is not iterative, it is very stable, it is not based on derivatives nor requires any threshold.

1. Introduction

Physical discontinuities, discretised as intensity variations, are particularly important in many vision tasks, such as edge detection, segmentation, and denoising. Detecting such image features can narrow the search space prior to higher layers. However it is not a straightforward task. Discontinuities are related to different imaging sources, ambient light, colour, shadows, etc. Moreover, there is a big conceptual gap in the image processing community's ideas of what are edges and regions. Unfortunately, early vague ideas addressing these definitions were left so open that a plenty of ``better'' and ``optimal'' algorithms were created, and none could see any way to assess their claims.

Therefore, the idea of denoising, keeping edges and smoothing within regions has been easily said than done. Here we present an interesting concept which encompass the idea of filtering out noise, whilst preserving discontinuities. This concept does not follow the traditional path of stating what is a ``real edge'', rather we ingeniously code both smoothing and noise estimation in a MDL framework.

We present an adaptive Gaussian filter that computes directly the local amount of Gaussian smoothing in terms of variance. It is not iterative, it is stable, does not require a gradient stopping function nor any threshold.

2. Denoising and edges

There is a vast amount of publications in image processing on noise reduction and edges. Among the more interesting proposals are [4,9,10,19]. Traditional algorithms like median or midpoint are usually competitive up to certain degree of Gaussian noise, however after crossing such a boundary these basic algorithms return poor images.

Anisotropic diffusions [10,11,19,20] and adaptive smoothing [14,15] are algorithms that apply successive masks, which are functions of local gradient. However, both algorithms share some drawbacks, such as: (i) a behaviour difficult to predict (e.g. similar initial values return different images), (ii) useless convergence (thus, we need to fit carefully the number of iterations), and (iii) noise and data are combined at every iteration, which in turn complicates a formal analysis. Further improvements to anisotropic diffusion have not supplied better perceptual results than the original idea [11], and new edge stopping functions have become more complex, and slower to compute.

Obviously, there is seldom a single scale that is appropriate for a complete image. However, there is one proposal [4] that computes a single global scale. Hence it cannot cope with spatially correlated noise (i.e. not adaptive). Moreover, it also cannot deal with low signal-to-noise ratios due to a high threshold on the ``confidence''. Another approach [9] computes a local estimate by maximising a measure of edge strengh over a scale space. However this estimation is based on high-order derivatives which are very sensitive to noise. Thus, the algorithm has local stability troubles, which enforces to apply a second algorithm. Therefore, it lacks robustness, and at the same time, hides the real output of the scale selection step.

Mathematicians have been working in the similar topic, that is boundary preserving smoothers, and robust estimation, where local M-smoothers and W-smoothers from robust statistics have created promising lines. Although, smoothing with local M-estimators is a cumbersome optimisation problem, it has been shown [16] that M-estimates converges to a robust W-estimator. Further research has shown [18] a bijective relation between M-smoothers and $sigma $-filters (e.g. [3]). Nevertheless, in the definition of a $sigma $-filter we need to define two variances (same case as bilateral filtering [17]), which in turn complicates the problem by tuning not only one, but two variances. Moreover, it has been proposed a chain of $sigma $-filters [1], where one is expected to supply not only two variances but a serie of pairs (stages) in certain ad-hoc order.

Despite these developments, few works have been addressing the point on when to stop the filtering, since all last estimators have a piecewise constant image as fixed point. Instead, we shall explain how to estimate a local $sigma $ with a non-interative algorithm.

There are many other interesting approaches which are less known in image processing, however a more complete but larger account of this work will be published elsewhere.

3. Adaptive Gaussian filtering

Many existing algorithms in image processing assume a scale for feature detection. This scale represents a compromise between localisation accuracy and noise sensitivity. Prior knowledge of scale is often not available or vary unpredictibly on scenes. Hence, several ideas build over this assumption fail when these filters face real images, instead we should not assume a fixed global variance (e.g. in Gaussian filtering). Here we present a method for estimating the local variance with no assumptions on scale.

Although the problem can be formulated from other points of view (e.g. [6]), in terms of Bayesian estimation is set as follows: maximising the likelihood of the observed image given the local scale, and minimising the residual.

Consider a stack of smoothed images in a linear scale-space, $I_{sigma_{1}}, I_{sigma_{2}}, ..., I_{sigma_{n}}$, which are computed by convolving the initial image I0 with a serie of increasing Gaussian kernels $G_{sigma}, sigma=sigma _{1},...,sigma_{n}$, where $I_{sigma}=I_{0}*G_{sigma}$. Thus, the objective is to choose the appropriate index ($sigma $) from the scale-space, at each pair x,y. The criterion for such selection is based on the Minimal Description Length principle [13,2], i.e. the less complex or minimal, and, at the same time, effective for describing the model.

A Gaussian filtering can be seen as:


 begin{displaymath}I_{0}(x,y) = underbrace{I_{sigma}(x,y)}_{Low-Pass} + underbrace{varepsilon_{sigma}(x,y)}_{Residual} end{displaymath} (1)

where the residual, called $varepsilon _{sigma }$, is the original image minus the smoothed image.

The idea of selecting the minimal description length has been successfully applied [5,6,8,12,22] in machine vision for balancing simplicity and accuracy. The minimal description length states that the optimal model deal with the minimum number of bits that are necessary for maximising the information associated to the model. That is, the maximum smoothness with a minimal residual. Rewriting (1) as description length (dl):


begin{displaymath}dl_{I_{0}(x,y)} = dl_{I_{sigma}(x,y)} + dl_{varepsilon_{sigma}(x,y)} end{displaymath}

3.1 Description length of $I_{sigma }$

It is not difficult to see that a measure of information, in bits, for I0 is greater than $I_{sigma }$, for $sigma > 0$. That is, any smoothed image has less information that the original one. Notice that a given image at the end is piecewise constant due to a large $sigma $. Thus, when $sigmarightarrowinfty$, the measure of information over $I_{sigma }$is minimal.

In order to calculate a fast approximation of the amount of information in $I_{sigma }$, we start with an ideal model of low-pass filtering. Considering the behaviour of amplitude (a) in space (x) and frequency (f) through the Scaling-Uncertainty Principle we get:


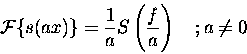
begin{displaymath}{cal{F}}{s(ax)} = frac{1}{a} Sleft( frac{f}{a} right) quad ; a ne 0 end{displaymath}

Therefore, a Gaussian distribution in space and frequency takes the form:


 begin{displaymath}e^{left(-frac{omega^{2}sigma^{2}}{2} right)} = e^{left(-frac{x^{2}}{2sigma^{2}}right)} quad ; sigma^{2} ne 0 end{displaymath} (2)

It is clear that the relation between the spatial domain ( $G_{sigma^{2}_{x}}$) is inversely proportional to frequency ( $G_{sigma^{2}_{omega}}$), then $sigma^{2}_{x} propto frac{1}{sigma^{2}_{omega}}$. Further, the sampling theorem states that for any signal of frequency f, the number of samples s(i.e. Nyquist rate) needed for reconstructing accurately the original signal is, at least, 2f. As we know $f propto sigma^{2}_{omega}$given a constant ($alpha$) to a Gaussian band-width, which is controlled by its variance $sigma^{2}_{omega}$. Thus, our sampling rate could be rewritten as $s = n(alphasigma^{2}_{omega}) quad ; n geq 2$.

Then, as a consequence of the inverse relation (2), we get that the amount of samples needed for describing a smoothed image is controlled by the spatial variance of a Gaussian kernel. That is:


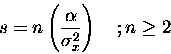
begin{displaymath}s = nleft(frac{alpha}{sigma^{2}_{x}}right) quad ; n geq 2 end{displaymath}

Although we cannot compute in advance how many bits represents each s, we effectively see that it is proportional ( $s propto bits$) to the amount of information, given a constant $beta$. Where $beta$is the precision, in bits, used to represent $I_{sigma }$. We can now summarise the above relations in the following equation:


 begin{displaymath}dl_{I_{sigma}} = nleft( frac{alphabeta}{sigma^{2}_{x}} right) quad ; n geq 2 end{displaymath} (3)

Equation (3) estimates the description length, in bits, of a smoothed image given the spatial variance of a Gaussian filter. In addition, equation (3) shows that a correct description length of $I_{sigma }$ is valid only within a range. The fact that n is unknown, does not, of course, mean that is not possible to estimate. Since $n geq 2$ we can inspect (visually) the number where n start. In this way, if we find the starting range, our algorithm becomes completely stable. Having calculated the first part of equation (1) we can compute the residual.

3.2 Description length of $varepsilon _{sigma }$

Even if we do not know the noise distribution, it approximates a Gaussian distribution by the Central Limit Theorem (zero-mean Gaussian density). Thus, the probability distribution of noise can be written as:


 begin{displaymath}Pr(varepsilon) = e^{- frac{varepsilon^{2}}{2sigma^{2}_{varepsilon}}} end{displaymath} (4)

where $sigma^{2}_{varepsilon}$ is the noise variance, and $varepsilon^{2}$ means the local quadratic residual1 between the original image, I0, and the filtered image $I_{sigma }$. As we have learnt from Shannon and Rissanen [13] works, the measure of information is closely related to the probability. Then, we can compute a measure of information in bits of equation (4), applying logarithm (log2). Thus, the description length of the residual takes the form of:


 begin{displaymath}dl_{varepsilon_{sigma}} = k left(frac{varepsilon^{2}}{2sigma^{2}_{varepsilon}}right) end{displaymath} (5)

where $k=frac{1}{ln 2}$. Once a $ld_{I_{sigma}}$ and $ld_{varepsilon_{sigma}}$ have been definited, we may, therefore, write the local description length as the sum of both terms, (3) and (5):


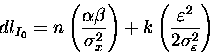
begin{displaymath}dl_{I_{0}} = nleft(frac{alphabeta}{sigma^{2}_{x}}right)... ...left(frac{varepsilon^{2}}{2sigma^{2}_{varepsilon}}right) end{displaymath}

Grouping terms, we have:


 begin{displaymath}dl_{I_{0}} = left(frac{lambda}{sigma^{2}_{x}}right) + varepsilon^{2} end{displaymath} (6)

where $lambda=frac{2nsigma^{2}_{varepsilon}alphabeta}{k}$. It is positive since that $n geq 2$ from equation (3), and the other constants are also positive. It is convenient to distinguish in equation (6), that $lambda$ represents, principally, the assumed noise variance $sigma^{2}_{varepsilon}$ and precision used to represent $I_{sigma }$. Thus, if we visually set $lambda$ to a high value, it will assume a high noise variance and precision, together to the starting range of n. Say, it is possible to recognise the starting range where $lambda$ becomes useful.

3.3 Final algorithm

Once equation (6) is defined, one may use it to estimate directly the local amount of smoothing in terms of variance, which is in fact an adaptive Gaussian filter. For every pair x,y compute2 $I_{0}, I_{sigma_{1}}, I_{sigma_{2}}, ... , I_{sigma_{n}}$. Then, based in the MDL principle, we choose the minimal value of $dl_{I_{sigma}}$ at each location x,y. This $min(dl_{I_{sigma}})$ estimates the optimal smoothness ( $sigma^{*}$) in x,y.

The local variance $sigma $ of a Gaussian at x,y, allows us the possibility of making an adaptive Gaussian filter. Each point x,y is smoothed as $sigma^{*}(x,y)$. That is,


begin{displaymath}hat{I}_(x,y) = I_{0}(x,y) * e^{left( -frac{x^{2}+y^{2}}{2sigma^{*}(x,y)}right)} end{displaymath}

3.4 Behaviour

Note that in the definition of equation (6) does not appear an edge stopping function nor gradient threshold. The minimal and maximal amount of smoothness are controlled by the $sigma_{min}$ and $sigma_{max}$ in the scale space. Moreover, an adaptive Gaussian filter (from 6) changes its shape ($sigma $) in the next way: if the filter is close to discontinuities, the MDL selects a $sigma $ closed to $sigma_{min}$; otherwise, if the filter is located in a uniform structure, the MDL selects a variance close to $sigma_{max}$. Notice that, a Gaussian shape ($sigma $) changes as a function of MDL. This is, in the neighbourhood of discontinuities the residual $varepsilon^{2}$grows much faster with respect to $sigma $ than in a relatively uniform region. As a result, the local scale selected will be small close to discontinuities, and large over uniform regions, which permits an effective noise elimination and an accurate discontinuity preservation.

4. Examples of adaptive Gaussian filtering

As an example, we filtered four images, figures (1a), (2a), (3a) and (4a) depict the input images which have been corrupted with Gaussian noise. Figures (1b), (2b), (3b) and (4b) depict the local scale map computed with equation (6). A value close to $sigma_{min}$ is darker. Following two panels (``c'' and ``d'') of every figure show the initial image after several iterations of a standard anisotropic diffusion algorithm3. Following panels (``e'') depict the correponding output of a chain of $sigma $-filters (so called non-linear Gaussian filters in [1]). The filter was tuned to five stages4 (chain length), $sigma_{x}=1.5$, and $sigma_{z}=30$, after spending a reasonable time over the three examples shown. Finally, panels ``f'' depic the adaptive Gaussian filter output after applying the scale map (panels ``b'') on the respective original image. Notice that the adaptive filter does not blur beyond regions nor across discontinuities. Moreover, it does not requiere any parameter nor threshold.

click here to see the examples

Images show that the adaptive Gaussian filter is very competitive or better than anisotropic diffusion or a chain of $sigma $-filters at a low computational cost, and with no supplying variables. As mentioned earlier, the algorithm is stable, i.e. not too dependent on the value of $lambda$. For instance, $lambda$ can be within a large range with the same performance. Presumably, the range where $lambda$ start is 3000, which is the value always used in our experiments. The algorithm took 3 seconds per image on an IBM H50 workstation, including disk access.

5. Conclusions and future work

We have presented an adaptive Gaussian filter that computes directly the local smoothing in terms of its variance. Which is by itself more intuitive than a successive application of weighted averaging masks or partial differential equations. The smoothness is computed in such a way that keeps the main discontinuities. Experiments show that the adaptive Gaussian filter is very competitive or better than anisotropic diffusion or a chain of $sigma $-filters at a low computational cost. In fact, our technique is not iterative, it is very stable nor requires any threshold.

These findings also suggest that this algorithm can contribute to the perception of different approaches, perhaps based on the MDL principle, to deal with local smoothing and feature extraction. Moreover, the MDL approach shows accurate results and could be a good way to substitute undesirable magic variables or thresholds in other low-level techniques.

Acknowledgments

The author wish to thank the CGC programme of the ETH-Zürich for supporting this research during 2000/2001.

Bibliography

1
V. Aurich, J. Weule, ``Non-Linear Gaussian Filters Performing Edge Preserving Diffusion'', Proc. of the 17th DAGM-Symposium, Bielefeld, 538-545, 1995.

2
A. Barron, J. Rissanen, B. Yu, ``The minimum description length principle in coding and modeling'', IEEE Trans. on Information Theory, vol. 44(6), pp. 2743-2760, Oct. 1998.

3
C.K. Chu, I.K. Glad, F. Godtliebsen, and J.S. Marron, ``Edge preserving smoothers for image processing'', JASA, 442(93), 526-541, June 1998.

4
J. Elder, S. Zucker, ``Local scale control for edge detection and blur estimation'', IEEE Trans. on PAMI, vol. 20(7), pp. 699-716, Jul. 1998.

5
G. Gomez, ``Local Smoothness in terms of Variance'', Proc. of the BMVC, vol. 2, pp. 815-824, Sep. 2000.

6
G. Gomez, J.L. Marroquin, L.E. Sucar, ``Probabilistic Estimation of Local Scale'', Proc. of the ICPR, vol. 3, pp. 798-801, Sep. 2000.

7
J.J. Koenderink, ``The structure of images''. Biological Cybernetics, vol. 50, pp. 363-370, 1984.

8
Y. Leclerc, ``Constructing simple stable descriptions for image partitioning''. IJCV, vol. 3(1), pp. 73-102, May 1989.

9
T. Lindeberg, ``Edge detection and ridge detection with automatic scale selection''. IJCV, vol. 30(2), pp. 117-156, Nov. 1998.

10
P. Perona, J. Malik, ``Scale space and edge detection using anisotropic diffusion''. IEEE Trans. on PAMI, vol. 12(7), pp. 629-639, July 1990.

11
P. Perona, T. Shiota, J. Malik, ``Anisotropic diffusion''. In B. M. ter Haar Romeny (ed.), Geometry-driven diffusion in computer vision, pp. 72-92. Dordrecht: Kluwer Academic Publishers, 1994.

12
M. Pilu, R. B. Fisher, ``Part segmentation from 2D edge images by the MDL criterion'', Image and Vision Computing, vol. 15(8), pp. 563-573, Aug. 1997.

13
J. Rissanen, ``A universal prior for integers and estimation by Minimum Description Length''. Annals of Statistics, vol. 11(2), pp. 416-431, 1983.

14
P. Saint-Marc, J. Chen, G. Medioni, ``Adaptive smoothing: a general tool for early vision''. Proc. of the Int. Conf. on CVPR, pp. 618-624, 1989.

15
P. Saint-Marc, J. Chen, G. Medioni, ``Adaptive smoothing: a general tool for early vision''. IEEE Trans. on PAMI, vol. 13(6), pp. 514-529, June 1991.

16
D. G. Simpson, X. He, Y-T Liu, ``Comment on: Edge-Preserving Smoothers for Image Processing'', JASA, 442(93), pp.544-548, June 1998.

17
C. Tomasi, R. Manduchi, ``Bilateral Filtering for Gray and Color Images'', Proc. of the ICCV, pp. 839-846, 1998.

18
G. Winkler, V. Liebscher, ``Smoothers for Discontinuous Signals'', to appear in J. of Nonpar. Statist.

19
J. Weickert, ``A review of nonlinear diffusion filtering''. In B. ter Haar Romeny, L. Florack, J. Koenderink, M. Viergever (Eds.), Scale-Space Theory in Computer Vision, Berlin: Springer-Verlag, LNCS 1252, pp. 3-28, 1997.

20
J. Weickert, ``Coherence-enhancing diffusion filtering''. IJCV, vol. 31, pp. 111-127, 1999.

21
A.P. Witkin, ``Scale-space filtering''. Proc. of the IJCAI, vol. 2, pp. 1019-1022, Aug. 1983.

22
H. Y. Zheng, S. Blostein, ``Motion-based object segmentation and estimation using the MDL principle'', IEEE Trans. on Image Processing, vol. 4(9), pp. 1223-1235, Sep. 1995.