Mutual Information For Evidence Fusion

Hannes Kruppa and Bernt Schiele
Perceptual Computing and Computer Vision Group
ETH Zurich, Switzerland
{kruppa,schiele}@inf.ethz.ch
http://www.vision.ethz.ch/pccv

In this tutorial a method for combining multiple object models is proposed based on the information-theoretic principle of mutual information. The ultimate goal is to make object detection more robust by using a combination of multiple object models. A case study in the context of face detection is presented. A more extensive account on this topic can be found in the full paper [2].

Mutual information has been used previously in computer vision, for example in image registration [4] or in audio-visual speech acquisition [3]. As detailed below, mutual information can be used to measure the mutual agreement between two object models. In order to combine multiple models a hierarchy of pairwise model combinations is used.

The mutual information of two random variables $X$ and $Y$ with a joint probability mass function $p(x,y)$ and marginal probability mass functions $p(x)$ and $p(y)$ is defined as [1]:

$$I(X;Y) = \sum_{x_i,y_j} p(x_i,y_j) log \frac{p(x_i,y_j)}{p(x_i)p(y_j)}$$ (1)

Here, the probabilities in expression 1 can be directly derived from a pair of distinct visual object models. To undermine the relevance of mutual information in the context of object model combination, we briefly refer to the well-known Kullback-Leibler divergence. The KL-divergence between a probability mass function $p(x,y)$ and a distinct probability mass function $q(x,y)$ is defined as:

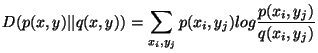$$D(p(x,y)\vert\vert q(x,y)) = \sum_{x_i,y_j} p(x_i,y_j) log \frac{p(x_i,y_j)}{q(x_i,y_j)}$$ (2)

Although the Kullback-Leibler divergence (also called relative entropy or information divergence) is not symmetric and does not satisfy the triangle inequality, it is often useful to think of it as a ``distance'' between distributions [1]. By defining $q(x,y) = p(x)p(y)$ the mutual information can be written as the KL-divergence between $p(x,y)$ and $p(x)p(y)$:

$$I(X;Y) = D( p(x,y) \vert\vert p(x)p(y) )$$ (3)

Mutual information therefore measures the ``distance'' between the joint probability $p(x,y)$ and the probability $q(x,y) = p(x)p(y)$, which is the joint probability under the assumption of independence. Conversely, it measures mutual dependency or the amount of information one object model contains about another. As a result mutual information can be used to measure mutual agreement between object models.

In the following we assume that for each subregion of the input image, each model determines the probability that the object of interest is either present or absent. This representation is very general and can be satisfied by nearly any object model. $p(x)$ is calculated based on the first object model and covers two cases, namely the presence of the object $p(x_0)$ or its absence $p(x_1) = 1-p(x_0)$, respectively. The probability $p(y)$ is derived from the second object model analogously, also with the two described cases. Finally, for the joint probability $p(x,y)$ both models and all four cases are taken into account.

Typically, the object of interest can be associated with a characteristic parameter range of an object model. For example, in the case of a color model, the parameter range may be given by a particular subspace of the total color-space. Note that each parameter configuration results in distinct probabilities $p(x)$ and $p(y)$ and consequently, in a distinct mutual information value. Therefore, one can determine a configuration $(\alpha^{\star},\beta^{\star})$ which maximizes mutual agreement between the employed models and the input data by maximizing the mutual information over the object-specific joint parameter space:

$$(\alpha^{\star},\beta^{\star}) = \arg I_{max}(X;Y) = \arg \max_{\alpha,\beta} I(X;Y)$$ (4)

with $\alpha$ and $\beta$ describing the object-specific parameter space of a model pair. For example the parameters of the facial shape model in the experiments described below are the size and the location of the face within the image. By maximizing mutual information with a second, complementary face model the algorithm detects and locates faces in the image. Figure 1 illustrates this concept.

Figure 1: (click here to enlarge) Maximization of Mutual Information: Each observed distribution is compared to the expected distribution that represents facial shape. In this particular example, the observed distribution comes from the skin color model applied to an input image with two faces. The mutual information between the two distributions is computed. The algorithm tries to maximize the mutual information by sampling the models' parameter spaces. As for the expected distribution, this means that the shown ``probability bump'' is deformable and can move over image coordinates. Likewise the skin color model's parameters are adapted by this procedure within appropriate bounds for skin detection.

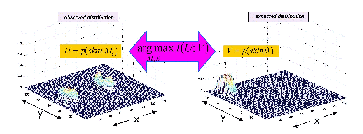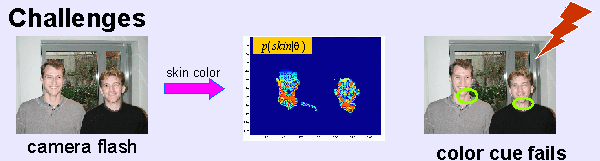
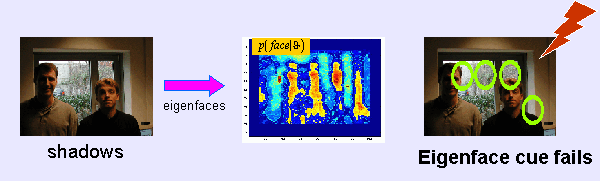
In order to combine multiple models a hierarchy of pairwise model combinations is used. At each stage the algorithm computes a ranking of parameter configurations which maximize mutual information. This ranking is then used as input for the next stage in the hierarchy where mutual information can be used again to find the best combined parameter configurations. The resulting algorithm is modular and can be easily extended to new object models. The hierarchical concept is depicted in figure 2 which shows the architecture used for face detection (see figures 3, 4, 5). In this case study, the following three object models are combined pairwise in order to detect human faces: a skin color model, a shape model and a template matcher. In stage one the probability maps are calculated based on the color model and the template matcher. Stage two combines the color model with the facial shape model by maximizing mutual information. The template matcher and the facial shape model are also combined in stage two. Finally stage three combines both results again by maximizing mutual information.

Obviously other groupings would be meaningful as well. The proposed grouping however ensures that the combined hypotheses on stage two can be represented as a single condensed region of probabilities. This will be further explained in the next sections. Also, it would be possible to combine all models in a single maximization step. However, using pairwise combinations enables the definition of separate and independent parameter constraints for each pair which reduces the size of the joint parameter space and therefore speeds up sampling.

Figure 2: (click here to enlarge) Multi-stage usage of maximization of mutual information for combining object models

Figure 3: The input image on the left was taken using a direct flashlight. As a result the fotograph is over-exposed. Column two in this figure shows the observed probability distributions when applying the skin color model. Column three shows detection results based on a combination of the color distribution and an oval facial shape model. While detection fails in this scenario both faces are safely located when all three models are combined. See Figure 5.

Figure 4: Challenging the template matcher: In this image light enters from the side which causes shadows on both faces. This situation poses a particular challenge to the template-based face model. The observed probability distribution from the template model is shown in the second column. Column three shows results after combination with the shape model. Many of these intermediate hypotheses are false positive detections. Even though the face template matcher fails the two faces are robustly detected by combining all three models together. See Figure 5.

Figure 5: This figure shows detection results combining all three models. The particular challenges posed in figures 3 and 4 are successfully dealt with.