Kernel Discriminant Analysis
Yongmin Li,
Shaogang
Gong and Heather Liddell
Department of Computer Science
Queen Mary, University of London
1. Introduction
For most pattern recognition problems, selecting
an appropriate representation to extract the most significant features
is crucially important. Principal Component Analysis (PCA) [8,10] has been widely adopted to
extract abstract features and to reduce dimensionality in many pattern
recognition problems. But the features extracted by PCA are actually
"global" features for all pattern classes, thus they are not
necessarily much representative for discriminating one class from
others. Linear Discriminant Analysis (LDA) [2,3,9], which seeks to find a linear
transformation by maximising the between-class variance and minimising
the within-class variance, has proved to be a suitable technique for
discriminating different pattern classes. However, both the PCA and
LDA are linear techniques which may be less efficient when severe
non-linearity is involved. To extract the non-linear principal
components, Kernel PCA (KPCA) [7] was developed using the
popular kernel technique [11,12]. However, similar to the linear
PCA, KPCA captures the overall variance of all patterns which are not
necessary significant for discriminant purpose. To extract the
nonlinear discriminant features, Kernel Discriminant Analysis (KDA)
[6,1,4], a nonlinear discriminating method
based on kernel techniques [11,12], was developed.
2. Kernel Discriminant Analysis
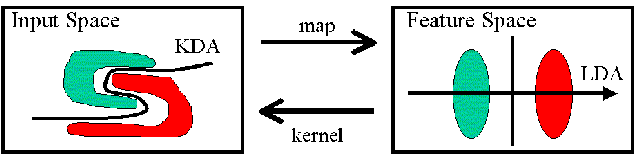
The principle of KDA can be
illustrated in Figure 1. Owing
to the severe non-linearity, it is difficult to directly compute the
discriminating features between the two classes of patterns in the
original input space (left). By defining a non-linear mapping from the
input space to a high-dimensional feature space (right), we (expect
to) obtain a linearly separable distribution in the feature
space. Then LDA, the linear technique, can be performed in the feature
space to extract the most significant discriminating
features. However, the computation may be problematic or even
impossible in the feature space owing to the high dimensionality. By
introducing a kernel function which corresponds to the non-linear
mapping, all the computation can conveniently be carried out in the
input space. The problem can be finally solved as an
eigen-decomposition problem like PCA, LDA and KPCA.
|
Figure 1: Kernel Discriminant Analysis.
3. A Toy Problem
We use a toy problem to illustrate the
characteristics of KDA as shown in Figure 2. Two classes of patterns
denoted by circles and crosses respectively have a significant
non-linear distribution. To make the results comparable among
different representations (PCA, LDA, KPCA and KDA), we try to separate
them with a one dimensional feature, i.e. the most significant
mode of PCA, LDA, KPCA or KDA. The first row shows the patterns and
the discriminating boundaries computed by each of the four different
methods. The second row illustrates the intensity of the
one-dimensional features given by PCA, LDA, KPCA and KDA on the region
covered by the training patterns.

|
Figure 2: Solving a nonlinear
classification problem with, from left to right, PCA, LDA, KPCA and
KDA. The first row shows the patterns and the discriminating
boundaries computed by each of the four methods. The second row
illustrates the intensity of the computed one-dimensional features on
the region covered by the training patterns.
4. Representing Multi-View Faces Using KDA
Face images with large pose variation demonstrate significant
nonlinearity, which makes face recognition a challenging problem. To
address this problem, we apply KDA to represent multi-view face
patterns.
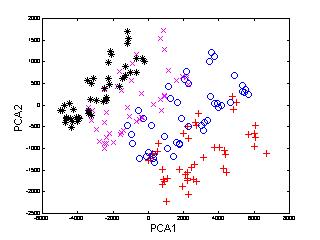
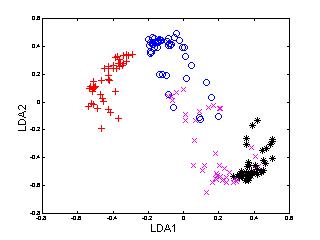
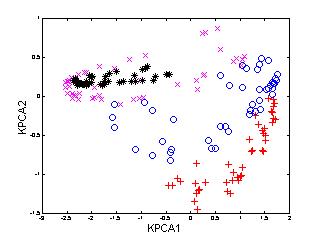
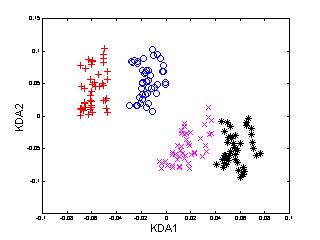
In the following example (Figure 3), 540 multi-view
face patterns from 12 subjects, 45 of each, were used to train
KDA. For the sake of clarity, only the patterns of first four face
classes are shown here. To compare the performance of KDA, we also
applied PCA, LDA and KPCA to the same set of face patterns.
|
Figure 3: Distribution of multi-view
face patterns in PCA, LDA, KPCA and KDA spaces (only the first two
dimensions).
It is noted that
-
the pattern distributions using PCA and KPCA are not satisfactorily separable,
or more precisely, the variation from different subjects is even overshadowed
by that of other sources, since these two techniques are not designed for
discriminating purpose;
-
LDA performs better than PCA and KPCA, but not as good as KDA;
-
KDA provides the best discriminating performance among the four
methods.
Yongmin Li 2001-10-14






