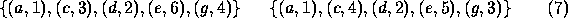Graph
Graph
Matching

It is possible to represent object models by a directed or undirected graph structure in which the set of nodes, 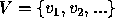 , represents labelled features of the model and the set of arcs,
, represents labelled features of the model and the set of arcs, 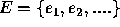 , represents relationships between them. Examples of directed arcs are relationships such as greater than, less than, whereas undirected arcs include relationships such as parallel and connected, equivalent to ordered and unordered relations respectively. In its purest form, two graphs,
, represents relationships between them. Examples of directed arcs are relationships such as greater than, less than, whereas undirected arcs include relationships such as parallel and connected, equivalent to ordered and unordered relations respectively. In its purest form, two graphs, 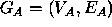 and
and 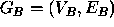 are isomorphic if there is a one-to-one mapping, f, such that
are isomorphic if there is a one-to-one mapping, f, such that
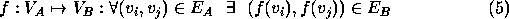
In other words, there is a correspondence between the nodes of 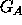 and
and 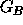 that preserves the arc relationships. However, in order to determine if two object models are equivalent, it is not sufficient to determine solely that the two graphs are isomorphic, but that the labelling of the arcs and nodes is also equivalent. In practical scene identification, each of the arcs and nodes generally assumes a value within a continuum, a line of length x pixels for example, and the elegance of the approach is sometimes lost.
that preserves the arc relationships. However, in order to determine if two object models are equivalent, it is not sufficient to determine solely that the two graphs are isomorphic, but that the labelling of the arcs and nodes is also equivalent. In practical scene identification, each of the arcs and nodes generally assumes a value within a continuum, a line of length x pixels for example, and the elegance of the approach is sometimes lost.
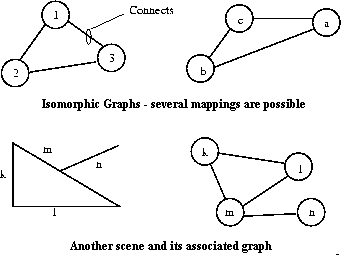
Figure 5: Graphs for the triangle problem
The graph isomorphism problem is of little practical use in scene analysis because it is not expected that the scene segmentation will be perfect. In addition to the problem of false or missing features, and hence node data, it is common that a multiple object scene is matched against single object models. One approach to scene interpretation using attributed relational graphs is to define a distance measure between two graphs in terms of the number of node or arc deletions, insertions or substitutions required in order to make the two graphs isomorphic. The identified object is the one with the smallest distance measure. This approach is clumsy and does not cater for multiple object scene analysis.
Therefore, in general, we wish to solve the subgraph isomorphism problem between a graph 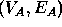 and a subgraph of another graph
and a subgraph of another graph 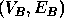 , or a subgraph of
, or a subgraph of 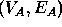 and a subgraph of
and a subgraph of 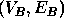 .
This is computationally harder than the isomorphic problem, because it is not known in advance which nodes and arcs form the respective subgraphs to be matched.
.
This is computationally harder than the isomorphic problem, because it is not known in advance which nodes and arcs form the respective subgraphs to be matched.
The maximal clique algorithm applied to an association graph is the most elegant solution to this problem. The association graph is formed by creating nodes from each compatible pair of scene and model features, 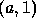 and so on, and inserting arcs between nodes if they have equivalent relations expressed as arcs. In order to illustrate this approach, we can re-examine the matching problem of Figures 3 and 4. An association node is formed if the lengths of two compared lines are within plus or minus 10% in terms of the number of pixels. An arc is established between nodes if two conditions are satisfied. Firstly, the corresponding scene and model features must have the same connectivity (to within 10 pixels). Secondly, the angular change between the two corresponding segments must be the same.
and so on, and inserting arcs between nodes if they have equivalent relations expressed as arcs. In order to illustrate this approach, we can re-examine the matching problem of Figures 3 and 4. An association node is formed if the lengths of two compared lines are within plus or minus 10% in terms of the number of pixels. An arc is established between nodes if two conditions are satisfied. Firstly, the corresponding scene and model features must have the same connectivity (to within 10 pixels). Secondly, the angular change between the two corresponding segments must be the same.
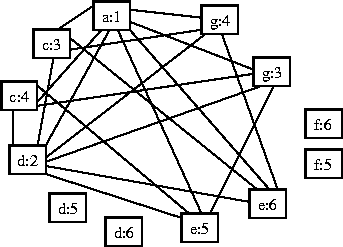
Figure 6: The association graph for the bracket problem
Assuming that the set of nodes, N, represents the association graph and 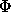 is the empty set, an algorithm for finding the set of all cliques may be expressed recursively.
is the empty set, an algorithm for finding the set of all cliques may be expressed recursively.
cliques(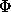 ,N); (* Initial call to recursive procedure *)
,N); (* Initial call to recursive procedure *)
cliques 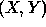 :=
IF no node in Y-X connected to all elements in X THEN
output X, which is a clique
ELSE
select a node y which is connected to all elements of X
cliques(
:=
IF no node in Y-X connected to all elements in X THEN
output X, which is a clique
ELSE
select a node y which is connected to all elements of X
cliques(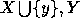 )
)  cliques(
cliques(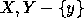 )
)
To find largest cliques, add an additional test in ``cliques'' to stop
the recursion if the number of nodes in X added to
the number of nodes in (Y - X) connected to all of X is less than k, where k is set initially to the largest possible clique. If no cliques of size
k are found, then decrement k and run cliques(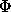 ,N) with the new value of k.
,N) with the new value of k.
This algorithm can be modified to find maximal cliques if, at
each recursive call to the cliques procedure, the set of nodes, 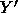 is computed such that
is computed such that
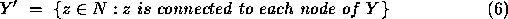
If 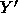 is not contained within Y, then the search may be terminated, since Y cannot then contain any maximal cliques. Another way of looking at
the same thing might be to check that y is not connected to every node in Y; if this is the case, then after removing y, Y cannot contain a maximal clique since any cliques found would have all elements connected to y.
is not contained within Y, then the search may be terminated, since Y cannot then contain any maximal cliques. Another way of looking at
the same thing might be to check that y is not connected to every node in Y; if this is the case, then after removing y, Y cannot contain a maximal clique since any cliques found would have all elements connected to y.
Yet again, it might be simpler just to run the clique algorithm to completion without checks. Maximal cliques are extracted by cross-checking; the largest maximal clique or cliques may be found readily since the largest clique must be maximal. Depending on the requirement this may be the quickest solution.
Examining Figure 6, above, the two largest maximal cliques are found,
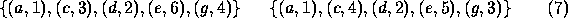
The two solutions reflect the constraints; the object is symmetrical !
Like the interpretation tree search, a disadvantage of the maximal clique approach is the complexity, exponential in the number of nodes. A solution to this is to restrict the matching process to smaller graphs, e.g. by considering only small groups of features in relative proximity, and concentrating on small sub-structures within the overall scene, the ``local-feature focus'' method.



[ Interpretation tree search |
Relaxation labelling ]
Comments to: Sarah Price at ICBL.
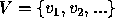 , represents labelled features of the model and the set of arcs,
, represents labelled features of the model and the set of arcs, 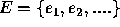 , represents relationships between them. Examples of directed arcs are relationships such as greater than, less than, whereas undirected arcs include relationships such as parallel and connected, equivalent to ordered and unordered relations respectively. In its purest form, two graphs,
, represents relationships between them. Examples of directed arcs are relationships such as greater than, less than, whereas undirected arcs include relationships such as parallel and connected, equivalent to ordered and unordered relations respectively. In its purest form, two graphs, 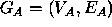 and
and 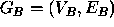 are isomorphic if there is a one-to-one mapping, f, such that
are isomorphic if there is a one-to-one mapping, f, such that


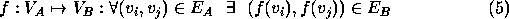
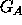 and
and 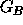 that preserves the arc relationships. However, in order to determine if two object models are equivalent, it is not sufficient to determine solely that the two graphs are isomorphic, but that the labelling of the arcs and nodes is also equivalent. In practical scene identification, each of the arcs and nodes generally assumes a value within a continuum, a line of length x pixels for example, and the elegance of the approach is sometimes lost.
that preserves the arc relationships. However, in order to determine if two object models are equivalent, it is not sufficient to determine solely that the two graphs are isomorphic, but that the labelling of the arcs and nodes is also equivalent. In practical scene identification, each of the arcs and nodes generally assumes a value within a continuum, a line of length x pixels for example, and the elegance of the approach is sometimes lost.

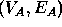 and a subgraph of another graph
and a subgraph of another graph 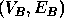 , or a subgraph of
, or a subgraph of 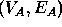 and a subgraph of
and a subgraph of 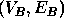 .
This is computationally harder than the isomorphic problem, because it is not known in advance which nodes and arcs form the respective subgraphs to be matched.
.
This is computationally harder than the isomorphic problem, because it is not known in advance which nodes and arcs form the respective subgraphs to be matched.
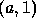 and so on, and inserting arcs between nodes if they have equivalent relations expressed as arcs. In order to illustrate this approach, we can re-examine the matching problem of
and so on, and inserting arcs between nodes if they have equivalent relations expressed as arcs. In order to illustrate this approach, we can re-examine the matching problem of 
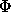 is the empty set, an algorithm for finding the set of all cliques may be expressed recursively.
is the empty set, an algorithm for finding the set of all cliques may be expressed recursively.
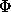 ,N); (* Initial call to recursive procedure *)
,N); (* Initial call to recursive procedure *)
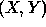 :=
IF no node in Y-X connected to all elements in X THEN
output X, which is a clique
ELSE
select a node y which is connected to all elements of X
cliques(
:=
IF no node in Y-X connected to all elements in X THEN
output X, which is a clique
ELSE
select a node y which is connected to all elements of X
cliques(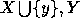 )
)  cliques(
cliques(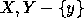 )
)
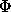 ,N) with the new value of k.
,N) with the new value of k.
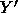 is computed such that
is computed such that
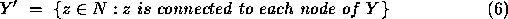
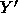 is not contained within Y, then the search may be terminated, since Y cannot then contain any maximal cliques. Another way of looking at
the same thing might be to check that y is not connected to every node in Y; if this is the case, then after removing y, Y cannot contain a maximal clique since any cliques found would have all elements connected to y.
is not contained within Y, then the search may be terminated, since Y cannot then contain any maximal cliques. Another way of looking at
the same thing might be to check that y is not connected to every node in Y; if this is the case, then after removing y, Y cannot contain a maximal clique since any cliques found would have all elements connected to y.