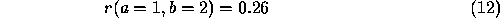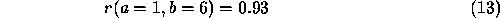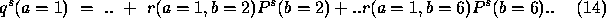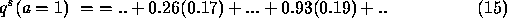Relaxation
Relaxation
Labelling

Relaxation labelling has been applied to many problems in computer vision, from edge detection to scene interpretation on the basis of labelled scene components. Early work on scene labelling of line drawings employed a discrete relaxation approach in which each scene component was assigned a set of possible interpretations, and inconsistent labellings were removed by examining firstly label pairs on connected segments, and by ensuring secondly that the locally defined consistencies could be linked together in a continuous closed path. This type of algorithm could be applied to scenes like the room in Figure 1
Assign all possible labels to each object
REPEAT
FOR each scene object
Delete inconsistent labels on the basis of unary constraints
Delete inconsistent labels on the basis of N-ary constraints
UNTIL (any object has no label) OR (no updating possible)
IF (any object unlabelled) THEN return no solution
ELSE return current solution
P>
The current solution may be a complete consistent labelling, as with Figure 1, or ambiguities may still remain. There may be more than one consistent labelling, as was seen (hopefully)
when we examined line labelling.
As an alternative to discrete relaxation, probabilistic relaxation allows each scene object
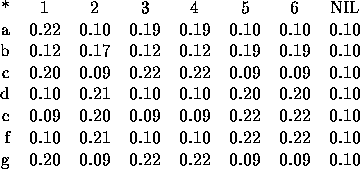
to have associated with it not only a set of component labels, but also a weighting assigned to each label in the range 0 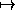 1.
In general, these weighting are considered as probabilities, and so the sum of the label probabilities should be equal to 1.0. There are several approaches to linear and non-linear probabilistic relaxation schemes; here we consider a linear relaxation scheme. In either case, the basic algorithm is
1.
In general, these weighting are considered as probabilities, and so the sum of the label probabilities should be equal to 1.0. There are several approaches to linear and non-linear probabilistic relaxation schemes; here we consider a linear relaxation scheme. In either case, the basic algorithm is
Define conditional probabilities for each label assignment to each component
REPEAT
FOR each scene object
update labellings on basis of compatibility function
UNTIL (a maximum of an objective function, F is reached)
OR (probabilities cease to change)
Return current solution
The initial conditional probabilities can be assigned (strictly using Bayes theorem) on the basis of the scene evidence. For example, if a given region of a room image is chequered there is a high condition probability that it is a floor,
P(floor||chequered) - 0.8, say, however, it might be a tablecloth.
P(cloth||chequered) - 0.2. The compatibility function is based on the interaction between scene objects, as before. For example, if a region A is above another region B in a room scene, then the labelling A=ceiling has a high compatibility with the labelling B=floor. We shall be more precise in a moment.
Generally, a relaxation process will find a local maximum in the particular criterion, F, defining the quality of match. There are two key issues in relaxation, first the rate of convergence
towards the maximum, and second the position of the local maximum in its particular optimisation space. Convergence can not always be guaranteed, and the algorithm may converge
to a local maximum, based for example on local consistency of several sets of scene objects, rather tahan of the scene as a whole. To move towards a globally optimum solution, it may be necessary to move through solutions which are locally sub-optimal. If a global maximum is required, a stochastic optimisation procedure may be more appropriate. In essence, this alters the probabilities with some degree of randomness every so often, to move from local valleys to a more global optimum.
We can now consider more fully the example of the Anadex printer bracket in
Figure 3.
We shall assign initial probabilities on the basis of length, so that the sum of the label weightings is 1.0 for each scene object or component.
We add a NIL label to allow for the fact that a scene object may be erroneous, and not part of any model. The NIL labelling is given an arbitrary value of 0.1, and the other values assigned according to a linear weighting scheme with a maximum value if the lengths are identical, and a minimum value if the model feature length is less than or equal to half the length of the scene feature, or greater than or equal to twice the scene length. This results in an initial ad hoc labelling as follows,
We now consider how the support function is calculated, and the set of probabilities updated in an iterative loop. A compatibility coefficient, r, is assigned between each pair of features.
In general, the support for the label 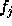 of component
of component 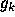 given by component
given by component 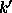 is
is
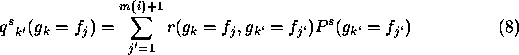
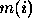 is the number of model labels, (1 ... 6 in this case), but an
additional NIL label is allowed.
The total support for this particular labelling from all components
in the network is given,
is the number of model labels, (1 ... 6 in this case), but an
additional NIL label is allowed.
The total support for this particular labelling from all components
in the network is given,
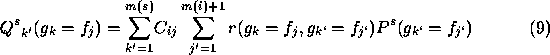
where 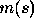 is the number of scene components, (a ... g in this case)
and
is the number of scene components, (a ... g in this case)
and 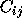 are weights satisfying
are weights satisfying
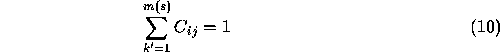
Usually, at least in examples like this, all scene components
will have equal weight so that 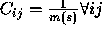 .
however, there may be occasions when particular scene components and
labels carry more weight.
The linear probability updating formula is,
.
however, there may be occasions when particular scene components and
labels carry more weight.
The linear probability updating formula is,
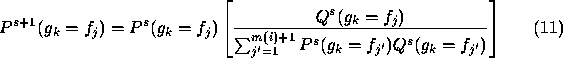
As discussed, continued iteration of the relaxation process converges to a local optimum
in the compatibility function expressed above. Where several maxima exist, it may or may not be appropriate to find a global optimum solution, depending on the particular application criteria.
A local optimum is more directly representative of the initial probability assignments, and hence of the measured properties of the constituent features of the description, whereas a global optimum is dependent primarily on the compatibility function, r.
We can now define a plausible support function for the bracket example.
Compatibility is based again on the geometric properties, in this case the required transformation to match the proposed scene features to their corresponding model features. Examining the relevant data on which
Figure 4 is based, we can determine the rotation about the origin followed by a translation in x and y required to superimpose each model on each scene feature. For example, the transformations, 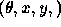 from segment a to segment 1 and segment b to segment 6 are (0,89,254) and (4,95,260) respectively, i.e. highly compatible. On the other hand, the transformation from b to 2 is (182,5,-18) which
is highly incompatible with the a to 1 transformation. Intuitively, it is reasonable to calculate a high value of the support function, close to 1.0, in the case where the two transformations are similar, and a low value close to 0.0 when they are widely different. A possible approach is to calculate the sum of the errors in x,y and (6 pixels, 6 pixels and 4 degrees respectively in the first instance) and apply a linear weighting so that a minimum compatibility of 0.0 corresponds to a total error of 200 units or greater. On this basis,
from segment a to segment 1 and segment b to segment 6 are (0,89,254) and (4,95,260) respectively, i.e. highly compatible. On the other hand, the transformation from b to 2 is (182,5,-18) which
is highly incompatible with the a to 1 transformation. Intuitively, it is reasonable to calculate a high value of the support function, close to 1.0, in the case where the two transformations are similar, and a low value close to 0.0 when they are widely different. A possible approach is to calculate the sum of the errors in x,y and (6 pixels, 6 pixels and 4 degrees respectively in the first instance) and apply a linear weighting so that a minimum compatibility of 0.0 corresponds to a total error of 200 units or greater. On this basis,
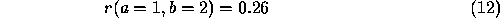
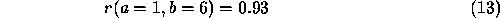
Thus the support for the labelling a=1 from node b is
given on the initial values by Equation 8, above, as
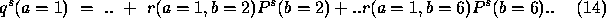
Substituting some real numbers,
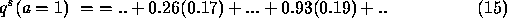
This process is successively applied according to equations 8 to 11 and the relaxation algorithm to arrive at a solution using an appropriate termination condition.
Very useful comments by Boris Flach
[There are also some] pitfalls of
the discrete relaxation labelling. Let me demonstrate the easiest
example.
Suppose we want to solve the usual graph coloring problem i.e. to
color the vertices of a graph such that no pair of adjacent vertices
are assigned the same color. If we have 3 colors and the graph is a
tetrahedron then there is no such coloring. Now let us solve this
problem using relaxation labelling by using labels corresponding to
the colors and binary constraints. Obviously realaxation labelling
stops after the first step and all labels remain undeleted. Does this
indicate that there are consistent labellings? No, of course not.
We can try to use not only binary constraints but also the resulting
ternary constraints and so on. But in this case the algorithm becomes
NP-complete and hence useless for real applications.
If the underlying graph of the problem is a partial m-tree
and has n vertices and there are k labels then an algorithm exists
scaling with (k^m)n.
On the other hand an algorithm scaling with (k^3)(n^3) is known, if
the constraints have some additional properties. The complexity of the
underlying graph is arbitrary in this case.
Summarizing, we should understand that the
usual relaxation labelling in general gives answers "yes", "no" and "I
dont know" on the question whether a consistent labelling exists for
a given problem.



[ Graph matching |
References ]
Comments to: Sarah Price at ICBL.
 1.
In general, these weighting are considered as probabilities, and so the sum of the label probabilities should be equal to 1.0. There are several approaches to linear and non-linear probabilistic relaxation schemes; here we consider a linear relaxation scheme. In either case, the basic algorithm is
1.
In general, these weighting are considered as probabilities, and so the sum of the label probabilities should be equal to 1.0. There are several approaches to linear and non-linear probabilistic relaxation schemes; here we consider a linear relaxation scheme. In either case, the basic algorithm is



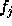 of component
of component 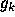 given by component
given by component 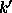 is
is
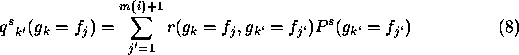
 is the number of model labels, (1 ... 6 in this case), but an
additional NIL label is allowed.
The total support for this particular labelling from all components
in the network is given,
is the number of model labels, (1 ... 6 in this case), but an
additional NIL label is allowed.
The total support for this particular labelling from all components
in the network is given,
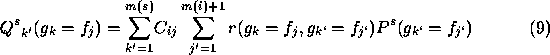
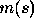 is the number of scene components, (a ... g in this case)
and
is the number of scene components, (a ... g in this case)
and 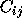 are weights satisfying
are weights satisfying
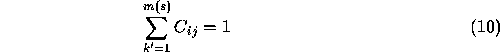
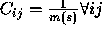 .
however, there may be occasions when particular scene components and
labels carry more weight.
The linear probability updating formula is,
.
however, there may be occasions when particular scene components and
labels carry more weight.
The linear probability updating formula is,
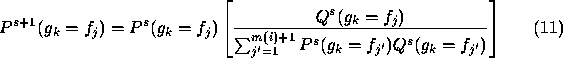
 from segment a to segment 1 and segment b to segment 6 are (0,89,254) and (4,95,260) respectively, i.e. highly compatible. On the other hand, the transformation from b to 2 is (182,5,-18) which
is highly incompatible with the a to 1 transformation. Intuitively, it is reasonable to calculate a high value of the support function, close to 1.0, in the case where the two transformations are similar, and a low value close to 0.0 when they are widely different. A possible approach is to calculate the sum of the errors in x,y and (6 pixels, 6 pixels and 4 degrees respectively in the first instance) and apply a linear weighting so that a minimum compatibility of 0.0 corresponds to a total error of 200 units or greater. On this basis,
from segment a to segment 1 and segment b to segment 6 are (0,89,254) and (4,95,260) respectively, i.e. highly compatible. On the other hand, the transformation from b to 2 is (182,5,-18) which
is highly incompatible with the a to 1 transformation. Intuitively, it is reasonable to calculate a high value of the support function, close to 1.0, in the case where the two transformations are similar, and a low value close to 0.0 when they are widely different. A possible approach is to calculate the sum of the errors in x,y and (6 pixels, 6 pixels and 4 degrees respectively in the first instance) and apply a linear weighting so that a minimum compatibility of 0.0 corresponds to a total error of 200 units or greater. On this basis,