The simplest aspect graph algorithms refer to orthographic projections of convex polyhedra. Here, there is just one type of accidental view, when a face of the object projects onto a line segment in the image. In this case, we can compute the partitioning of viewpoint space from the planes of the polyhedron. This forms either great circles on a viewing sphere, or planes in 3D space, surrounding the object.

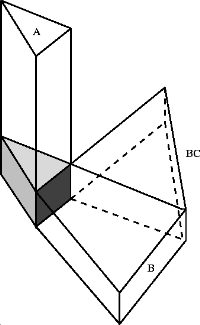
Figure 2: Subdivision of 3D viewpoint space for a convex polyhedron

Figure 2, above, illustrates how cells are formed in 3D space for a simple wedge shaped object. A full aspect graph for a tetrahedron is shown in Figure 3, below. ( [References, no 1]).

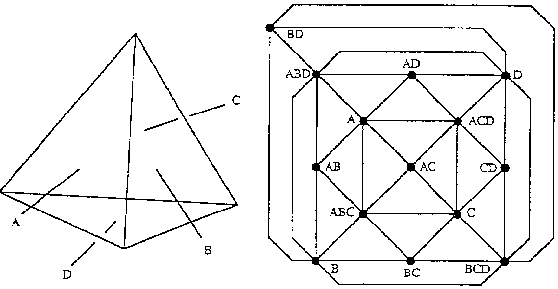
Figure 3: The aspect graph of a tetrahedron

For more general polyhedra, different visual events can occur, edge vertex and edge triplet alignments, illustrated in Figures 4, below, and 5 ([References: no 2]).

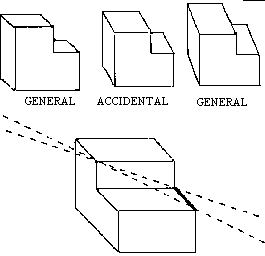
Figure 4: Accidental alignment of contour and vertex

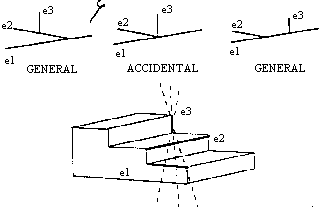
Figure 5: Accidental alignment of three contours

Hence, to compute the aspect graph for more general polyhedra, we need to enumerate all possible boundary-vertex and boundary triplet alignments. For a viewing sphere the results are great circles and quadric curves, for a 3D space, planes and quadric surfaces. As an example, there is a plane in 3D space which corresponds to the set of accidental viewpoints from which the boundary and vertex of Figure 4 can be viewed simultaneously. The equation of this plane can be computed from the equation of the line and the point position; i.e. both the line and point lie in that plane.

In general the viewpoint space will be ``over-partioned'' by enumerating the coincident planes of all boundaries and vertices, and the coincident quadrics of triple boundaries. First, several of these visual events may be occluded for opaque objects. Second, boundaries have finite length, so that alignments only exist on a portion of the total plane or quadric. Hence, some ``extra'' processing is required that can determine or reduce the degree of over-partitioning of viewpoint space. A simple example may illustrate this. Considering the L-shaped wedge of Figure 4 we could form a convex polyhedron by stretching 3 planes over the concave volume, then compute the exact aspect graph. Then, we need only consider further the region of viewpoint space from which at least one of these planes can be seen. We enumerate the possible alignments of the edges and vertices surrounding the concave volume to further partion the view space.

As mentioned above, the same esential strategy is adopted for computing aspect graphs of any class of object considered in the literature. The main variations and difficulties lie in the determination of all possible visual events, a task which becomes increasingly hard as more complex shapes are considered.