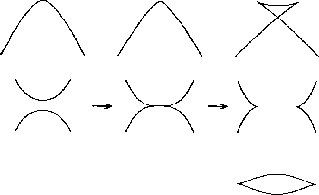
Figure 6: Local singularities: top - swallowtail, middle - beak-to beak, bottom - lip
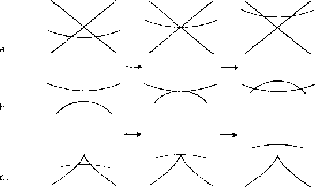
Figure 7: Multilocal singularities: top - triple point, middle - tangent crossing, bottom - cusp crossing


Determining an exhaustive catalogue of visual events for curved objects proves more complex than for polyhedra. All visual events for polyhedra are viewpoint-dependent and can be determined from an object model. Curved objects introduce a new class of viewpoint-dependent visual events, created by the object limb or rim (the locus of points where the line of sight is tangential to the surface). Due to symmetry the viewpoint space of solids of revolution is partitioned in bands identified by only one parameter.
Kriegman and Ponce (See ref. 3) report an implemented technique for computing the exact orthographic aspect graph of solids of revolution. Singularity theory is employed to create a catalogue of visual events. Views are projections of limbs (occluding contours) and creases (intersections of surface patches). The authors assume algebraic curves as solid generators and orthographic projections. Each step of the three-step algorithm presented corresponds to solving a system of polynomial equations, using both symbolic methods (elimination theory) and numerical methods (continuation).

Figure 6: Local singularities: top - swallowtail, middle - beak-to beak, bottom - lip

Figure 7: Multilocal singularities: top - triple point, middle - tangent crossing, bottom - cusp crossing
Singularities depend on the shape of the contour and the viewing direction; for example a series of singular views of an opaque vase are shown in Figure 8, below. The circular-symmetric aspect graph is shown in Figure 9 (See ref. 3 Kriegman and Ponce, 1990).



[ Polyhedral objects |
Piecewise smooth objects ]
Comments to: Sarah Price at ICBL.