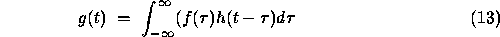


The convolution integral is expressed in one dimension by the relationship
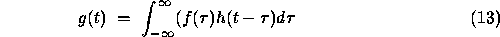
This represents the convolution of two time functions, 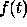 and
and
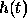 ; commonly
; commonly 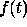 is a time varying signal, e.g. speech, and
is a time varying signal, e.g. speech, and 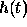 is the impulse (time) response of a particular filter.
is the impulse (time) response of a particular filter.  is a dummy
variable which represents the shift of one function with respect to
the other, as illustrated in
Figure 7: Convolution in One Dimension
is a dummy
variable which represents the shift of one function with respect to
the other, as illustrated in
Figure 7: Convolution in One Dimension
The importance of the convolution integral is based to a large extent on the
convolution theorem
which relates multiplication in the time domain to convolution in the frequency
domain and vice versa.
Representing the convolution of two functions by the symbol 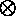 , then
, then
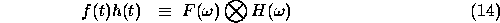
and
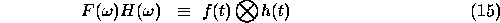
In 2-dimensional image processing terms, the continuous convolution integral may be expressed
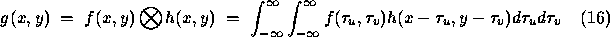
In a manner analagous to one-dimensional convolution, the function 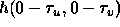 is simply the image function
is simply the image function 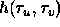 rotated by 180 degrees about the origin.
The function
rotated by 180 degrees about the origin.
The function 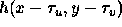 is the function further translated to move the
origin of the image function g to the point
is the function further translated to move the
origin of the image function g to the point 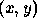 in the
in the 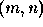 plane.
The functions are then pointwise multiplied and the product function is
integrated over 2 dimensions.
Convolution of digital sampled images is analagous to that for continuous
images, except that the integral is transformed to a discrete summations
over the image dimensions, m and n.
plane.
The functions are then pointwise multiplied and the product function is
integrated over 2 dimensions.
Convolution of digital sampled images is analagous to that for continuous
images, except that the integral is transformed to a discrete summations
over the image dimensions, m and n.
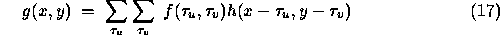
Since both 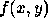 and
and 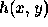 are non-zero over a finite
domain, i.e. the field of view of the imaging system, the summation
is necessary only over the area of non-zero overlap.
The number of required multiply and add operations is equal to the number
of pixels in
are non-zero over a finite
domain, i.e. the field of view of the imaging system, the summation
is necessary only over the area of non-zero overlap.
The number of required multiply and add operations is equal to the number
of pixels in 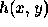 times the number of pixels in
times the number of pixels in 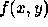
Hence an algorithm for digital convolution of an image 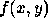 of pixel
dimensions p by q with a mask,
of pixel
dimensions p by q with a mask, 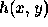 of dimensions 2m+1 by 2n+1,
is expressed,
of dimensions 2m+1 by 2n+1,
is expressed,
For each row, i =1 to p
For each column, j =1 to p
(* Process pixel
*)
Set output image pixel,
=0
For each mask row, k=-m to m
For each mask column, l=-n to n
=
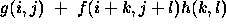


[ Quantisation, Sampling and Noise |
Smoothing and Edge Enhancement by Convolution ]

Comments to: Sarah Price at ICBL.
(Last update: 4th July, 1996)