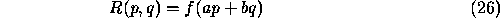
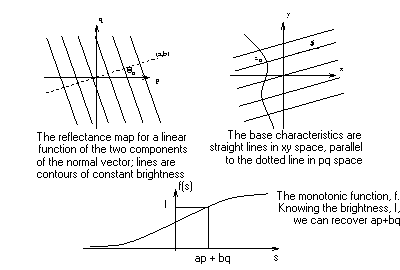
Figure 6: The linear reflectance map, and the monotonic function f
First, consider a reflectance map which is a linear combination of p and q, illustrated in Figure 6, below and expressed as
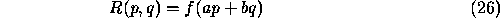
Figure 6: The linear reflectance map, and the monotonic function f
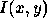at a point we can determine directly the value of ap+bq from the inverse of the function 
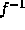. Hence we have (as before) one constraining equation on the values of p and q.
Now, the slope of the surface at an angle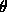 
to the x-axis is
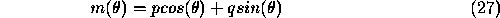
Choose a particular direction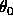 
where 
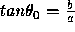, perpendicular to the iso-brightness contours, along the line of steepest ascent(descent) of the reflectance function.
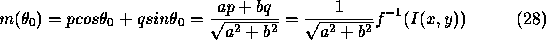
since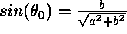 
and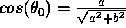 
.
However, in the linear case, we know that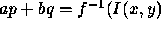 
so we can determine the
slope directly in this particular direction from Equation. This is the key to the method of characteristic strip expansion. Knowing the reflectance function, we take a small step 
in the direction of greatest brightness change in the image function,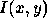 
. This produces a change in depth, z of 
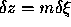. The direction of movement in the image plane is parallel to the direction of of the line through 
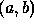in the gradient space. Hence,
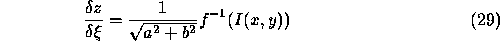
where
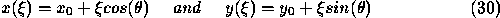
Integrating Equation 28,
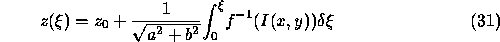
This gives the basic algorithm for shape recovery.
Start the solution at a known point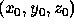
REPEAT
Take a small step
along a characteristic strip
along the line of steepest descent of the image function
Calculate the new
from Equation 30 Calculate
from Equation 31 Reset start point to
UNTIL ( a discontinuity is reached in the image function)
To recover the shape of a whole surface, we need several strips; this implies that we need several starting points. From each starting point we explore the surface along the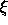 
direction. However, in general, the reflectance map is not linear, so that the characteristic strips are not straight lines in image space.
[ Recovering shape from shading |
The general case ]
Comments to: Sarah Price at ICBL.