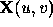 , illustrated in Figure 2, from Equation 8, the x component is simply u, the y component is v and the z component is
, illustrated in Figure 2, from Equation 8, the x component is simply u, the y component is v and the z component is 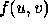 . The first fundamental form, I is defined
. The first fundamental form, I is defined


There are two classical quadratic forms used in the analysis of smooth surfaces, the first and second fundamental forms.
Knowledge of these forms provides an analysis and classification of surface shape. For a given surface or surface patch, 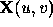 , illustrated in Figure 2, from Equation 8, the x component is simply u, the y component is v and the z component is
, illustrated in Figure 2, from Equation 8, the x component is simply u, the y component is v and the z component is 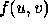 . The first fundamental form, I is defined
. The first fundamental form, I is defined
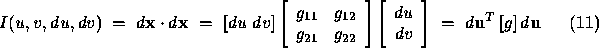
where
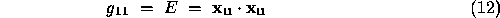
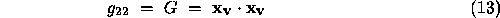
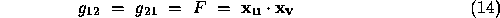
The subscripts denote partial differentiation
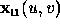 and
and 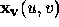 define the tangent vectors
to the surface at the point
define the tangent vectors
to the surface at the point 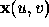 , as illustrated
in Figure 2, see link above. They form the basis of the tangent plane which touches the surface at point
, as illustrated
in Figure 2, see link above. They form the basis of the tangent plane which touches the surface at point 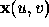 .
.  is the first fundamental form matrix, the metric or the metric tensor of the surface. The first fundamental form,
is the first fundamental form matrix, the metric or the metric tensor of the surface. The first fundamental form,  , is a measure
of the amount of movement of a surface at the coordinates
, is a measure
of the amount of movement of a surface at the coordinates 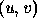 in the parameter plane. It is invariant to translations and rotations of the surface in 3D space, and thus is an intrinsic parameter of the surface.
in the parameter plane. It is invariant to translations and rotations of the surface in 3D space, and thus is an intrinsic parameter of the surface.
The second fundamental form is dependent on the position of the surface in 3D space. Thus it is an extrinsic property of the surface. This is given by
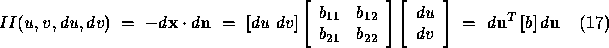
where the 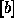 matrix elements are
matrix elements are
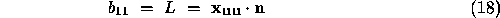
The double subscripts denote second partial derivatives.
and the unit normal vector
The second fundamental form matrix,
the maximum principal curvature occurs for a small movement of the normal vector ``around the cylinder'', i.e. perpendicular to the cylinder axis. The minimum principal curvature occurs for a small movement ``along the cylinder'', i.e parallel to the cylinder axis; in fact it is zero.
Comments to: Sarah Price at ICBL.
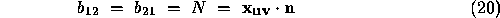
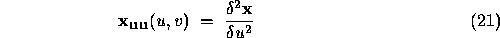
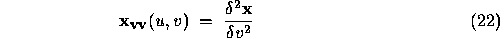
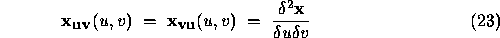
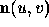 is
is

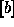 , measures the
change in normal vector
, measures the
change in normal vector  and the change of surface position
and the change of surface position
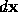 at a surface point at
at a surface point at 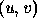 as a function of a small movement
as a function of a small movement 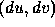 in the parameter space. The differential normal vector
in the parameter space. The differential normal vector
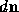 always lies in the tangent plane. The ratio
always lies in the tangent plane. The ratio 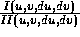 is the normal curvature function,
is the normal curvature function, 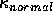 , which
varies only as a function of the differential vector
, which
varies only as a function of the differential vector 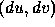 . If
. If  and
and  are aligned for a particular direction of
are aligned for a particular direction of 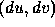 then that direction is a principal direction of the surface at that surface point. The extrema of the normal curvature function occur at that point and are called the principal curvatures,
then that direction is a principal direction of the surface at that surface point. The extrema of the normal curvature function occur at that point and are called the principal curvatures, 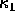 the maximum and
the maximum and 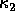 the minimum. For example, consider the cylinder of Figure 1:
the minimum. For example, consider the cylinder of Figure 1:
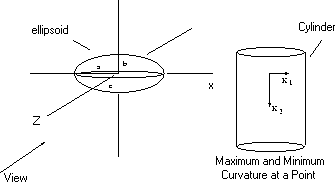
Figure 1: Viewing an ellipsoid: Principal curvatures of a cylinder



[ Surface definition |
Mean and Gaussian curvature ]