Our idea is to use the most stable Hilbert's invariants:
the ones which involve only derivatives till
order ``one''.
If we had to deal with gray level images, we should have obtained
only 2 invariants, which is of course not enough to characterize
correctly points of interest,
we show in this paper that this very poor characterization is widely compensated by color information.
It means that using three image planes, a simple extension of grey level invariants
gives us 6 invariants: 3 intensities and 3 gradient magnitudes plus 2 color specific additional
invariants (Invariant theory says that we must have 
invariants at order one).
Now the vector of invariants against translation and rotation obtained contains 8 components.
We call it: 
.
The reader can compare the feature vectors 
obtained for two points correctly matched at
figures 1 and 2.
Using only first order invariants instead of invariants till second order presents
two main advantages:
, 
, 
, 
,
, 
, 
, 
,
, 
, 
, 
,
, 
),
second order needs much more, (this feature is important as we use
sub-pixel Gaussian filtering [11]).
Figure 1: Two matched Harris points in left and right images Lizard differing from a rotation of
90 
.
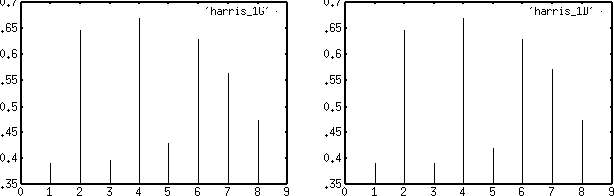
Figure: Feature vectors of point n 1 in images Lizard. The derivatives
are computed using a Gaussian filter with 
= 3. We see clearly that
the eight invariants
computed are invariant to rotation.
