 |
Because very little is known about how the brain processes visual information, we will instead look at the computer-vision paradigm and highlight methods of computation that are biologically inspired. Much that is done in computer vision has an engineering approach - that is, find a solution, regardless of how it relates to any biological system. However, there are some techniques in computer vision that are inspired by what is known about how biological systems function, and it is these analogies that we shall draw upon in the following lectures.
The next five lectures will concentrate on classical image processing techniques, both in the spatial and the frequency domain. We will begin with binary images, where the mathematical modelling is simplest. Most industrial applications of computer vision still attempt to extract as much information as possible from an impoverished binary image, and indeed much can be done with this data. Thus, lecture 2 will cover the geometrical and topological properties of binary images and closely follows chapters 2 and 3 of Horn's ``Robot Vision'' [4]. Continuing with image topology in lecture 3, we will also study connected components and the theory of morphology, as developed by Serra [8]. Gonzalez and Woods' ``Digital Image Processing'' [3] covers this work in Chapter 8. Fourier theory is introduced in lecture 4, and then the image enhancement techniques developed in lectures 5 and 6 are also covered by Gonzalez and Woods.
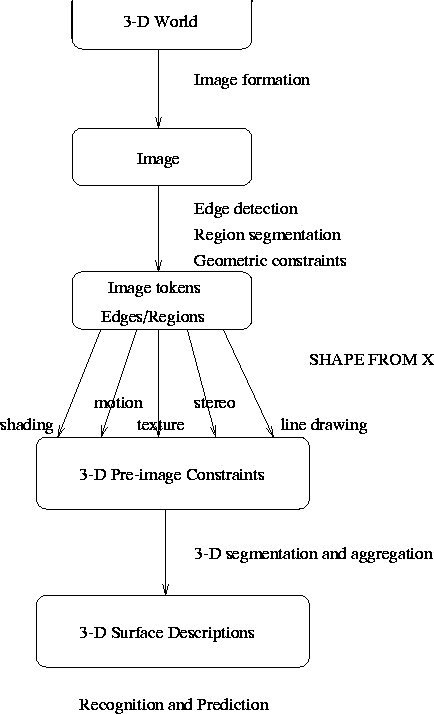
In the computer-vision paradigm (see Figure 6), an image is first acquired and then some form of data-reduction is performed to help in the subsequent analyses. This in itself is biologically inspired: the retina has something like 120 million rods and 5 million cones, but the total number of nerve fibres leaving the eye is only about 1 million. Some form of compression must be applied very early in visual processing; the compressed format must be high in information, and low in redundancy, whereas we know that raw image data is highly redundant.
Most researchers agree that the early stages in vision perform some sort of edge detection (lecture 7). In lectures 8-10 we will study one particular model of edge detection, known as the local energy model. Aspects of this model that are biologically inspired will be outlined, along with their mathematical foundations.
Following the data compression stages, image interpretation needs to be undertaken. How do we infer information about the 3D world from mere 2D projections? Mathematicians would say that the problem is ill-posed, in the sense that there is an infinite number of solutions or interpretations, but the physical constraints imposed by the real world limit these interpretations substantially. Thus, after the compression stage comes a series of modular, but perhaps interlinked, stages of what is known as Shape-from-X. Examples include shape from stereo, shape from motion, shape from texture, or shape from shading. In all these cases, additional information renders an ill-posed problem soluble, and allows us to interpret the 3D geometry of the scene under view.
Having obtained the 3D geometry of the scene under view, we then need to interpret it, or match it with our existing knowledge of the world. We understand what it is we see, even when we see that object from a completely novel view. In order to match the geometry of the objects in our scene with that of the objects in our known database, we use invariants, that is geometrical descriptions of the object that are invariant to the types of transformations that the visual process performs.
In lectures 11-13 we will consider the problems of calibration, stereo and motion, and comment upon the biologically plausible nature of their solution. We will also briefly outline the recognition process that then follows, given either the 3D data constructed by the stereo module, or using geometric information directly available from the 2D scenes.