Image formation in the eye and the camera

Biological vision is the process of using light reflected from the surrounding world as a way of modifying behavior. Generally, with humans, we say that the surrounding environment is interpreted by visual input. This usually implies some form of conscious understanding of the 3D world from the 2D projection that it forms on the retina of the eye. However much of our visual computation is carried out unconsciously and often our interpretations can be fallacious.

In this section we will briefly overview the human visual system and try to understand the ways in which this system uses computation as a means of interpreting its input. To do this, we will also try to understand how images are formed on cameras, how images are stored in computers, and how computations can be carried out efficiently. Although not strictly correct, this analogy between machine vision and biological vision is currently the best model available. Moreover, the models interact in an ever increasing fashion: we use the human visual system as an existence proof that visual interpretation is even possible in the first place, and its response to optical illusions as a way to guide our development of algorithms that replicate the human system; and we use our understanding of machine vision and our ability to generate ever more complex computer images as a way of modifying, or evolving, our visual system in its efforts to interpret the visual world. For example, image morphing scenes would be difficult to interpret for the naive viewer.

The eye

Any understanding of the function of the human eye serves as an insight into how machine vision might be solved. Indeed, it was some of the early work by Hubel and Wiesel [5] on the receptive fields in the retina that has led to the fundamental operation of spatial filtering that nowadays dominates so much of early image processing. There are many good references to the function of the eye, although Frisby [2] gives an excellent overview with a computational flavour.

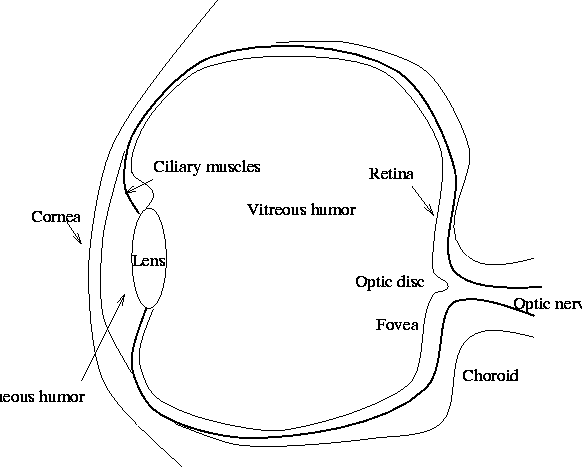
The eye is considered by most neuroscientists as actually part of the brain. It consists of a small spherical globe of about 2cm in diameter, which is free to rotate under the control of 6 extrinsic muscles. Light enters the eye through the transparent cornea, passes through the aqueous humor, the lens, and the vitreous humor, where it finally forms an image on the retina (see Figure 1).

 

Figure: Sketch of a cross-section of the eye (schematic after Nalwa).

It is the muscular adjustment of the lens, known as accommodation, that focuses the image directly on the retina. If this adjustment is not correctly accomplished, the viewer suffers from either nearsightedness or farsightedness. Both conditions are easily corrected with optical lenses.

The retina itself is a complex tiling of photoreceptors. These photoreceptors are known as rods and cones. When these photoreceptors are stimulated by light, they produce electrical signals that are transmitted to the brain via the optic nerve. The location of the optic nerve on the retina obviously prohibits the existence of photoreceptors at this point. This point is known as the blind spot and any light that falls upon it is not perceived by the viewer. Most people are unaware of their blind spot, although it is easy to demonstrate that it exists. And its existence has been known about for many years as it is reputed that the executioners in France during the revolution used to place their victim so that his or her head fell onto the blind spot, thus illiciting a pre-guillotine perception of the poor character without a head.

The rods and cones do not have a continuous physical link to the optic nerve fibres. Rather, they communicate through three distinct layers of cells, via junctions known as synapses. These layers of cells connect the rods and cones to the ganglion cells, which respond to the photostimulus according to a certain receptive field. We can see from Figure 2 that the rods and cones are at the back of the retina. Thus the light passes through the various cell layers to these receptive fields, and is then transmitted via various synaptic junctions back towards the optic nerve fibre.

 

Figure: Schematic of a cross section of the retina (after Nalwa).

It has long been known that the spatial organization of some of the receptive fields of the retinal ganglion cells is circularly symmetric, with either an excitatory central region and an inhibitory surround, or with an inhibitory centre and an excitatory surround. Such cells are known to computational vision researchers as ``mexican-hat operators''. Their existence inspired Marr [6] to develop a computational approach to physiological vision understanding, since their response to a light signal was analogous to the convolution of the signal with the second derivative of a Gaussian. Marr's theory of edge detection will be explored in a later lecture.

However, there are also other spatial organisations of receptive fields. There are orientationally selective receptive fields, with an excitatory lobe to one side and an inhibitory lobe on the other, so as to form an antisymmetric field. These cells exist over a wide variety of orientations. Both the even and odd symmetric receptive fields are known as simple cells. They respond strongly to luminance edges and line features in images, respectively.

Other types of receptive fields, known as complex cells, are also found in the retina. Their behaviour is more complex, combining in a non-linear fashion the responses of the even and odd symmetric filter responses. And end-stopped cells appear to act as simple differentiation operators. How the behaviour of these cells might be combined into a single computational model will be outlined in a future lecture.

The human eye is a remarkable organ, whose sensitivity and performance characteristics approach the absolute limits set by quantum physics. The eye is able to detect as little as a single photon as input, and is capable of adjusting to ranges in light that span many orders of magnitude. No camera has been built that even partially matches this performance.

Very little is known about what happens to the optic signal once it begins its voyage down the optic nerve (see Figure 3). The optic nerve has inputs arriving from both the left and right sides of both eyes, and these inputs split and merge at the optic chiasma. Moreover, what is seen by one eye is slightly different from what is seen by the other, and this difference is used to deduce depth in stereo vision. From the optic chiasma, the nerve fibres proceed in two groups to the striate cortex, the seat of visual processing in the brain. A large proportion of the striate cortex is devoted to processing information from the fovea.

 

Figure: Overview of the visual pathways from eyes to striate cortex (schematic after Nalwa).

Camera models

To understand how vision might be modeled computationally and replicated on a computer, we need to understand the image acquisition process. The role of the camera in machine vision is analogous to that of the eye in biological systems.

Pinhole camera model

The pinhole camera is the simplest, and the ideal, model of camera function. It has an infinitesimally small hole through which light enters before forming an inverted image on the camera surface facing the hole. To simplify things, we usually model a pinhole camera by placing the image plane between the focal point of the camera and the object, so that the image is not inverted. This mapping of three dimensions onto two, is called a perspective projection (see Figure 4), and perspective geometry is fundamental to any understanding of image analysis.

 

Figure: Perspective projection in the pinhole camera model.

Perspective geometry

Euclidean geometry is a special case of perspective geometry, and the use of perspective geometry in computer vision makes for a simpler and more elegant expression of the computational processes that render vision possible. A superb overview of the geometric viewpoint in computer vision is given by Faugeras [1].

A perspective projection is the projection of a three-dimensional object onto a two-dimensional surface by straight lines that pass through a single point. Simple geometry shows that if we denote the distance of the image plane to the centre of projection by f, then the image coordinates (x_i,y_i) are related to the object coordinates (x_o,y_o,z_o) by

$x_i = \frac{f}{z_o} x_o$ and $y_i = \frac{f}{z_o} y_o$.

These equations are non-linear. They can be made linear by introducing homogeneous transformations, which is effectively just a matter of placing the Euclidean geometry into the perspective framework. Each point (x,y,z) in three-space is mapped onto a line in four-space given by (wx,wy,wz,w), where w is a dummy variable that sweeps out the line ($w \neq 0$). In homogeneous coordinates, the perspective projection onto the plane is given by

$$\begin{array} {ccccc} \left[ \begin{array} {c} x_i \\ y_i... ...x_o \\ y_o \\ z_o \\ w_o \end{array} \right] & .\end{array}$$

We now introduce some notation that will be useful in latter sections. The projective plane is used to model the image plane. A point in the plane is represented by a 3-vector (x₁, x₂, x₃) of numbers not all zero. They define a vector x up to a scale factor. A line l is also defined by a triplet of numbers (u₁, u₂, u₃), not all zero, and satisfies the equation u₁x + u₂y + u₃ = 0.

A point on a line is given by the relations

$${\bf l} . {\bf x} = 0 ~~ {\rm or} ~~ {\bf l}^T{\bf x} = 0 ~~ {\rm or } ~~ {\bf x}^T {\bf l} = 0.$$

Two points define a line by the equation ${\bf l} = {\bf p} \wedge {\bf q}$,where $\wedge$ denotes the vector product. Likewise, two lines define a point by the equation ${\bf x} = {\bf l} \wedge {\bf m}$. This duality between lines and points in the image plane is often exploited in homogeneous notation.

As well, a vector product can also be written in matrix notation, by writing the vector as a skew-symmetric matrix. Thus,

$${\bf v} \wedge {\bf x} = \left[ \begin{array} {ccc} 0 & -v_... ..._z & 0 & -v_x \\ -v_y & v_x & 0 \end{array} \right] {\bf x}.$$

Likewise, projective space is used as a model for Euclidean 3-space. Here, points and planes are represented by quadruplets of numbers not all zero, and are duals of each other.

Simple lens model

In reality, one must use lenses to focus an image onto the camera's focal plane. The limitation with lenses is that they can only bring into focus those objects that lie on one particular plane that is parallel to the image plane. Assuming the lens is relatively thin and that its optical axis is perpendicular to the image plane, it operates according to the following lens law:

$$\frac{1}{u} + \frac{1}{v} = \frac{1}{f},$$

where u is the distance of an object point from the plane of the lens, v is the distance of the focussed image from this plane, and f is the focal length of the lens (see Figure 5).

 

Figure: Simple lens model.

Camera calibration

To deduce three-dimensional geometric information from an image, one must determine the parameters that relate the position of a point in a scene to its position in the image. This is known as camera calibration. Currently this is a cumbersome process of estimating the intrinsic and extrinsic parameters of a camera. There are four intrinsic camera parameters: two are for the position of the origin of the image coordinate frame, and two are for the scale factors of the axes of this frame. There are six extrinsic camera parameters: three are for the position of the center of projection, and three are for the orientation of the image plane coordinate frame. However, recent advances in computer vision indicate that we might be able to eliminate this process altogether. These new approaches will be discussed in a later lecture.