The problem in object recognition is to determine which, if any, of a given set of objects appear in a given image or image sequence. Thus object recognition is a problem of matching models from a database with representations of those models extracted from the image luminance data. Early work involved the extraction of three-dimensional models from stereo data, but more recent work has concentrated on recognizing objects from geometric invariants extracted from the two-dimensional luminance data.
Of course, the representation of the object model is extremely important. Clearly, it is impossible to keep a database that has examples of every view of an object under every possible lighting condition. Thus, object views will be subject to certain transformations; certainly perspective transformations depending on the viewpoint, but also transformations related to the lighting conditions and other possible factors.
Two approaches have been developed to deal with the many possible transformations that an object may undergo in the imaging process: firstly, determine the transformation in question and then try and undo its effects, and secondly, find measurements of the object that are invariant to these types of transformations.
There are two stages to any recognition system. The first is the acquisition stage, where a model library is constructed from certain descriptions of the objects. The second is recognition, where the system is presented with a perspective image and determines the location and identity of any library objects in the image.
Generally, the most reliable type of object information that is available from an image is geometric information. So object recognition systems draw upon a library of geometric models, containing information about the shape of known objects. Usually, recognition is considered successful if the geometric configuration of an object can be explained as a perspective projection of a geometric model of the object.
All object recognition systems contain the following modules to some extent:
This problem, also known as the perceptual grouping problem, aims to organise the features that come from a single object into a single set. The types of features considered might be edges, corners, lines, curves represented as splines, or regional features such as texture. The grouping is usually accomplished using cues such as proximity, parallelism, collinearity, and continuity in curvature.
Thus object recognition is a process of hypothesizing an object-to-model correspondence and then verifying that the hypothesis is correct. Generally an hypothesis is considered successful if the error between the projected model features and the corresponding image features is below some threshold, and a reasonable fraction of the object outline is covered by the image features.
For the two approaches mentioned above, that of estimating the
transformation undergone in the imaging process has complexity
![]() , where
, where ![]() is the number of models,
i is the number of image features, m is the number of features per
model, and k is the number of features needed to determine the
object-image transformation. Typically, k is about 4.
is the number of models,
i is the number of image features, m is the number of features per
model, and k is the number of features needed to determine the
object-image transformation. Typically, k is about 4.
The approach that uses transformation-invariant measurements of the object in the image for recognition has complexity O(ik), where k is the number of features required to form the indexing. In this case, recognition need not be proportional to the number of models in the library. This can be a considerable advantage when the number of models is large.
An invariant of a geometric configuration is a function of the configuration whose value is unchanged by a particular transformation. For example, the distance between two points is unchanged for a Euclidean transformation (translation or rotation).
There are a number of geometric invariants for perspective transformations. Here we will illustrate just one of them, the cross-ratio of four points on a line.
Suppose we are given a configuration of four points on a line, as shown in Figure 6.
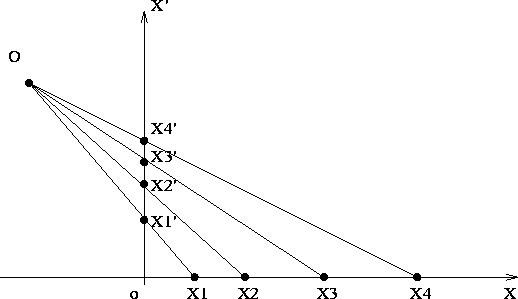 |
The ratio of ratios of lengths on the line, called the cross-ratio, is given by
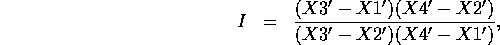
where X1', X2', X3', and X4' represent the corresponding positions of each point along the line.
The perspective transformation between the lines X and X' is given by
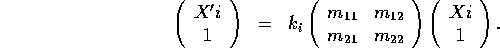
Now to see why the cross-ratio of four points on a line is preserved under such a transformation we note that the distance (Xi' - Xj') can be written as a determinant:
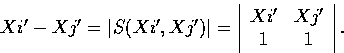
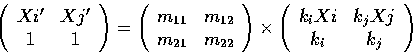
|S(Xi', Xj')| = kikj|M|.|S(Xi, Xj)|.
Substituting this relation into the expression for the cross-ratio gives
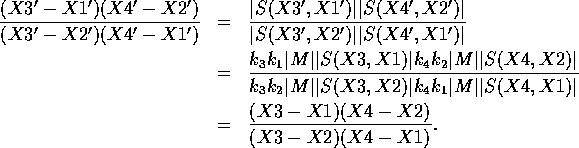
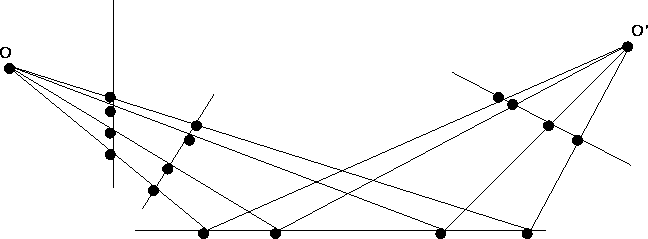
In summary, the cross-ratio is an invariant of any sets of four collinear points in projective correspondence. It is unaffected by the relative position of the line or the position of the optical centre, as shown in Figure 7.
 |
There are two stages to model-based recognition using invariants: