The value of a pixel with coordinates (x,y) in the enhanced
image ![]() is the result of performing some operation on
the pixels in the neighbourhood of (x,y) in the input image, F.
is the result of performing some operation on
the pixels in the neighbourhood of (x,y) in the input image, F.
Neighbourhoods can be any shape, but usually they are rectangular.
The simplest form of operation is when the operator T only acts on
a ![]() pixel neighbourhood in the input image, that is
pixel neighbourhood in the input image, that is
![]() only depends on the value of F at (x,y). This is a
grey scale transformation or mapping.
only depends on the value of F at (x,y). This is a
grey scale transformation or mapping.
The simplest case is thresholding where the intensity profile is replaced by a step function, active at a chosen threshold value. In this case any pixel with a grey level below the threshold in the input image gets mapped to 0 in the output image. Other pixels are mapped to 255.
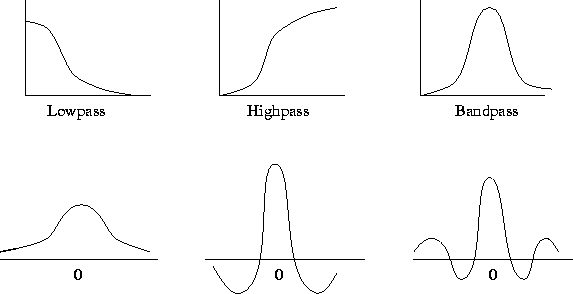
Other grey scale transformations are outlined in figure 1 below.
 |
How do we determine this grey scale transformation function? Assume our grey levels are continuous and have been normalized to lie between 0 and 1.
We must find a transformation T that maps grey values r in the input
image F to grey values s = T(r) in the transformed image ![]() .
.
It is assumed that
r = T-1(s).
If one takes the histogram for the input image and normalizes it so that the area under the histogram is 1, we have a probability distribution for grey levels in the input image Pr(r).
If we transform the input image to get s = T(r) what is the probability distribution Ps(s) ?
From probability theory it turns out that
![]()
Consider the transformation
![]()
![]()
![]()
We first need to determine the probability distribution of grey levels in the input image. Now
![]()
The transformation now becomes
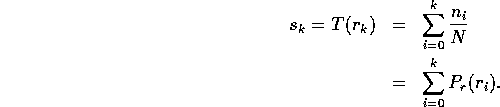
Note that ![]() , the index
, the index ![]() ,and
,and ![]() .
.
The values of sk will have to be scaled up by 255 and rounded to the nearest integer so that the output values of this transformation will range from 0 to 255. Thus the discretization and rounding of sk to the nearest integer will mean that the transformed image will not have a perfectly uniform histogram.
The aim of image smoothing is to diminish the effects of camera noise, spurious pixel values, missing pixel values etc. There are many different techniques for image smoothing; we will consider neighbourhood averaging and edge-preserving smoothing.
Each point in the smoothed image, ![]() is obtained from the average
pixel value in a neighbourhood of (x,y) in the input image.
is obtained from the average
pixel value in a neighbourhood of (x,y) in the input image.
For example, if we use a ![]() neighbourhood around each pixel
we would use the mask
neighbourhood around each pixel
we would use the mask
Each pixel value is multiplied by ![]() , summed, and then the
result placed in the output image. This mask is successively moved
across the image until every pixel has been covered. That is, the image
is convolved with this smoothing mask (also known as a spatial
filter or kernel).
, summed, and then the
result placed in the output image. This mask is successively moved
across the image until every pixel has been covered. That is, the image
is convolved with this smoothing mask (also known as a spatial
filter or kernel).
However, one usually expects the value of a pixel to be more closely related to the values of pixels close to it than to those further away. This is because most points in an image are spatially coherent with their neighbours; indeed it is generally only at edge or feature points where this hypothesis is not valid. Accordingly it is usual to weight the pixels near the centre of the mask more strongly than those at the edge.
Some common weighting functions include the rectangular weighting function above (which just takes the average over the window), a triangular weighting function, or a Gaussian.
In practice one doesn't notice much difference between different weighting functions, although Gaussian smoothing is the most commonly used. Gaussian smoothing has the attribute that the frequency components of the image are modified in a smooth manner.
Smoothing reduces or attenuates the higher frequencies in the image. Mask shapes other than the Gaussian can do odd things to the frequency spectrum, but as far as the appearance of the image is concerned we usually don't notice much.
Neighbourhood averaging or Gaussian smoothing will tend to blur edges because the high frequencies in the image are attenuated. An alternative approach is to use median filtering. Here we set the grey level to be the median of the pixel values in the neighbourhood of that pixel.
The median m of a set of values is such that half the values in the
set are less than m and half are greater.
For example, suppose the pixel values in a ![]() neighbourhood
are (10, 20, 20, 15, 20, 20, 20, 25, 100). If we sort the values we
get (10, 15, 20, 20, |20|, 20, 20, 25, 100) and the median here is
20.
neighbourhood
are (10, 20, 20, 15, 20, 20, 20, 25, 100). If we sort the values we
get (10, 15, 20, 20, |20|, 20, 20, 25, 100) and the median here is
20.
The outcome of median filtering is that pixels with outlying values are forced to become more like their neighbours, but at the same time edges are preserved. Of course, median filters are non-linear.
Median filtering is in fact a morphological operation. When we erode an image, pixel values are replaced with the smallest value in the neighbourhood. Dilating an image corresponds to replacing pixel values with the largest value in the neighbourhood. Median filtering replaces pixels with the median value in the neighbourhood. It is the rank of the value of the pixel used in the neighbourhood that determines the type of morphological operation.
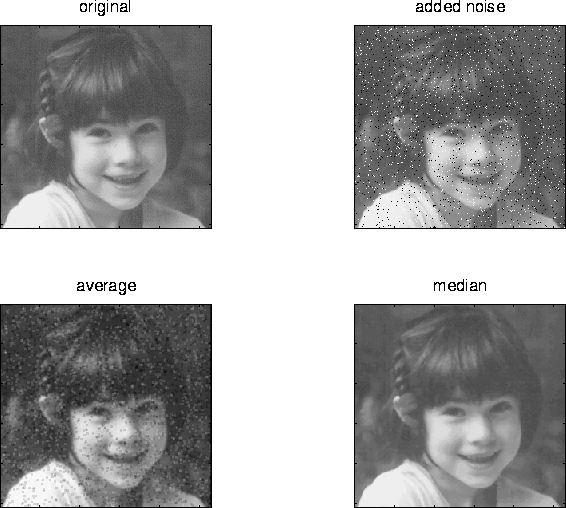 |
 |
Since the sum of all the weights is zero, the resulting signal will have
a zero DC value (that is, the average signal value, or the coefficient
of the zero frequency term in the Fourier expansion). For display
purposes, we might want to add an offset to keep the result in the
![]() range.
range.
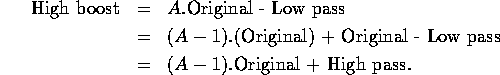
Now, if A = 1 we have a simple high pass filter. When A > 1 part of the original image is retained in the output.
A simple filter for high boost filtering is given by
| -1/9 | -1/9 | -1/9 |
| -1/9 | -1/9 | |
| -1/9 | -1/9 | -1/9 |
where ![]() .
.