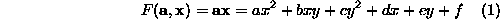
Let us represent a generic conic as the zero set of an implicit second order polynomial:
where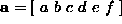 
and 
. 
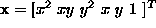is called the ``algebraic distance''
of a point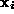 
to the conic 
.
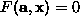One way of fitting a conic is to minimise the algebraic distance over the set of N data points in the least squares sense, that is
Linear conic fitting methods have been investigated that used linear constraints that slightly bias conic fitting towards elliptical solutions. In particular Rosin [8] and Gander [4] investigated the constraint a+c=1 and Rosin [7] f=1.
In a seminal work, Bookstein [1] showed that if a
quadratic constraint is set on the parameters (e.g., to avoid the
trivial solution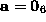 
) the minimisation (2)
can be solved by the rank-deficient generalised eigenvalue system:
where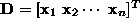 
is called design
matrix,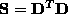 
is called scatter matrix and
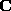is the matrix that expresses the constraint.
A simple constraint is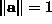 
but Bookestein used the
algebraic invariant constraint 
;
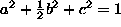Sampson [10] presented an iterative improvement to
Bookstein method that replaces the algebraic distance (1)
with a better approximation to the geometric distance, which was
adapted by Taubin [11] to turn the problem again into
a generalised eigen-system like (3).
Despite the amount of work, direct specific ellipse fitting, however, was left unsolved. If ellipses fitting was needed, one had to rely either on generic conic fitting or on iterative methods such as [6]. Recently Rosin [9] re-iterated this problem by stating that ellipse-specific fitting is essentially a non-linear problem and iterative methods must be employed for this purpose. In the following we show that this is no longer true.
