Department of Computer Science, Queen Mary and Westfield College, England
{jpmetal,sgg}@dcs.qmw.ac.uk
Yogesh Raja - Shaogang Gong
Mixture Models are a type of density model which comprise a number of component functions, usually Gaussian. These component functions are combined to provide a multimodal density. They can be employed to model the colours of an object in order to perform tasks such as real-time colour-based tracking and segmentation [1]. These tasks may be made more robust by generating a mixture model corresponding to background colours in addition to a foreground model, and employing Bayes' theorem to perform pixel classification. Mixture models are also amenable to effective methods for on-line adaptation of models to cope with slowly-varying lighting conditions [2].
Mixture models are a semi-parametric alternative to non-parametric histograms [3] (which can also be used as densities) and provide greater flexibility and precision in modelling the underlying statistics of sample data. They are able to smooth over gaps resulting from sparse sample data and provide tighter constraints in assigning object membership to colour-space regions. Such precision is necessary to obtain the best results possible from colour-based pixel classification for qualitative segmentation requirements.
Once a model is generated, conditional probabilities can be computed for colour pixels [1, 4]. Gaussian mixture models can also be viewed as a form of generalised radial basis function network in which each Gaussian component is a basis function or `hidden' unit. The component priors can be viewed as weights in an output layer. Finite mixture models have also been discussed at length elsewhere [3, 5, 6, 7, 8, 9, 10] although most of this work has concentrated on the general studies of the properties of mixture models rather than developing vision models for use with real data from dynamic scenes.
Let the conditional density for a pixel
belonging to a multi-coloured object 
be a mixture with M component densities:
where a mixing parameter P(j) corresponds to the prior
probability that pixel was generated by
component j and where 
. Each mixture component
is a Gaussian with mean 
and covariance matrix 
, i.e. in the case of a 2D colour space:
Figure 1 shows an example of a Gaussian mixture model of a multi-coloured object in HS-space.
Expectation-Maximisation (EM) [3, 11] is a well established maximum likelihood algorithm for fitting a mixture model to a set of training data. It should be noted that EM requires an a priori selection of model order, namely, the number of M components to be incorporated into the model. Often a suitable number may be selected by a user, roughly corresponding to the number of distinct colours appearing in an object to be modelled. The problem of fully automating this process, known as Automatic Model Order Selection, has been addressed in [12].
Figure 1 shows a Gaussian Mixture generated for a multi-coloured drinks can. Figure 2 illustrate pixel classification by combining foreground and background colour models to create a decision boundary in HS colour space. Bayes' theorem is employed to assign foreground or background membership to pixels.
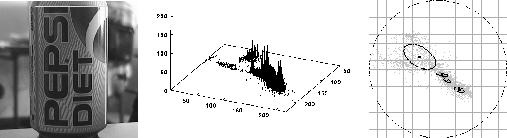
Figure 1: Left: a multi-coloured object (a PEPSI can). Centre: its
colour histogram in HS-space. It can be noted that such a histogram
representation is only viable when a large amount of data is available due
to being non-parametric. Right: its Gaussian mixture model. The mixture
components are shown as elliptical contours of equal probability.
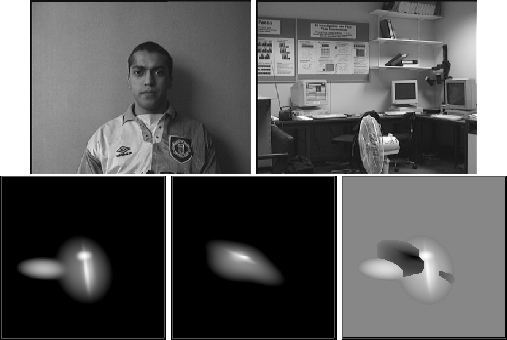
Figure 2: Colour mixture models of a multi-coloured object
(person model) and the context (scene model). The first row shows the data
used to build the foreground (person) and the background (laboratory)
models. The second row illustrates the probability density estimated from
mixture models for the object foreground and scene background. The
rightmost image is the combined posterior density in the HS colour
space. Here the ``bright'' regions represent foreground whilst the
``dark'' regions give the background. The ``grey'' areas are regions of
uncertainty.