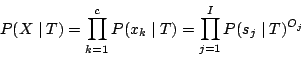 |
(3) |
where ![]() is the number of occurrence of
is the number of occurrence of ![]() in the observation
vector
in the observation
vector ![]() , so that we have
, so that we have ![]() . This
would lead to the
following equation for the posterior probability of the texture
parameters,
. This
would lead to the
following equation for the posterior probability of the texture
parameters,
![]() :
:
If on the other hand there is no a priori knowledge about ![]() or
equivalently
or
equivalently ![]() , the above formula should be integrated over
the
set of all possible textures,
, the above formula should be integrated over
the
set of all possible textures, ![]() :
:
where the last equality come from the law of succession.This result can be applied recursively to the whole sequence to calculate the conditional probability of each new observation given the preceding observations Algorithm 1.