
Next: Texture Boundary
Detection by
Up: Texture Estimation
Previous: texture
represented by histograms.
In the case of non-parametric representation of the texture and by
assuming independent probabilities for the observed pixels ( 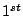 order Markovian model). For a first order Markov process, the 0th
order statistics of the samples must be an Eigenvector of
order Markovian model). For a first order Markov process, the 0th
order statistics of the samples must be an Eigenvector of 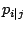 with Eigenvalue
with Eigenvalue 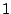 . Unfortunately, this means that a uniform
prior
for
. Unfortunately, this means that a uniform
prior
for 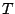 over
over 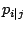 is
inconsistent with the uniform prior used in
the 0th order case. To re-establish the consistency, it is necessary
to choose a
is
inconsistent with the uniform prior used in
the 0th order case. To re-establish the consistency, it is necessary
to choose a 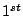 order prior such that the expected
value of a
column of the transition matrix
order prior such that the expected
value of a
column of the transition matrix 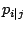 is
obtained by adding
is
obtained by adding 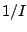 rather than 1 to the number of observations in that column of the
transition matrix before normalizing the column to sum to
rather than 1 to the number of observations in that column of the
transition matrix before normalizing the column to sum to 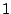 . This
means that the transition matrix,
. This
means that the transition matrix,
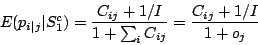 |
(6) |
where 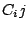 is
the number of times that intensity
is
the number of times that intensity 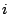 follows intensity
follows intensity
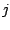 in the
sequence
in the
sequence 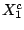 .
And hence the expected 0th order
distribution
(which is the vector
.
And hence the expected 0th order
distribution
(which is the vector 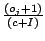 ) has the
desired
properties since:
) has the
desired
properties since:
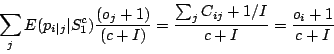 |
(7) |
Which is the
same as Equation 5. This
modification is equivalent to
imposing a prior over 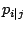 that favors structure
in the Markov
process and is proportional to
that favors structure
in the Markov
process and is proportional to 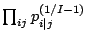 ). This
gives Algorithm 2.
). This
gives Algorithm 2.



Next: Texture Boundary
Detection by
Up: Texture Estimation
Previous: texture
represented by histograms.
Ali Shahrokni
2004-06-21