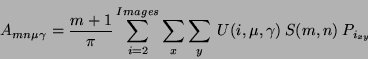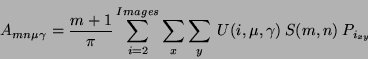

Next: Bibliography
Up: Velocity moments
Previous: Cartesian Velocity Moments
The new Zernike velocity moments [3] are expressed as:
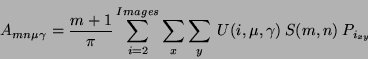 |
(19) |
They are bounded by
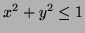 , while the shape's structure contributes through the orthogonal polynomials:
, while the shape's structure contributes through the orthogonal polynomials:
![\begin{displaymath}
S(m,n)~=~[V_{mn}(r,\theta)]^{*}
\end{displaymath}](img66.png) |
(20) |
Velocity is introduced as before (Equation 15),
while normalisation is produced by:
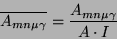 |
(21) |
The coordinate values for
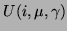 are calculated using the Cartesian moments and then translated to polar coordinates. If we consider first the
are calculated using the Cartesian moments and then translated to polar coordinates. If we consider first the  direction case only, from Equation 8 the angle
direction case only, from Equation 8 the angle 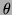 for a difference in
for a difference in 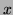 position is either
position is either 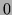 or
or  radians. The value used is dependent on the direction of movement. If the movement is in the positive
radians. The value used is dependent on the direction of movement. If the movement is in the positive 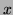 direction (or left to right) then:
direction (or left to right) then:
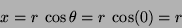 |
(22) |
where  is the length of the vector from the previous COM (Centre of Mass - as defined by the first order Cartesian moment) to the current COM, ie the velocity in pixels/image. Alternatively, if the movement is in the negative
is the length of the vector from the previous COM (Centre of Mass - as defined by the first order Cartesian moment) to the current COM, ie the velocity in pixels/image. Alternatively, if the movement is in the negative 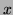 direction (or right to left) then:
direction (or right to left) then:
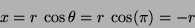 |
(23) |
The mapping to polar coordinates results in a sign change which could be used to detect the direction of motion.
Similarly for the 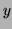 direction velocity, the values of
direction velocity, the values of 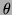 are either
are either 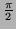 or
or
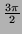 radians, and using Equation 8 produces:
radians, and using Equation 8 produces:
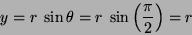 |
(24) |
and
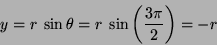 |
(25) |


Next: Bibliography
Up: Velocity moments
Previous: Cartesian Velocity Moments
Jamie Shutler
2001-09-25