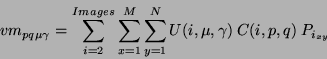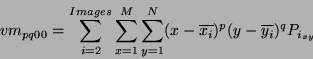

Next: Zernike Velocity Moments
Up: Velocity moments
Previous: Velocity moments
The Cartesian velocity moments [4] are computed from a sequence of images as:
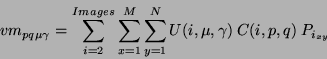 |
(13) |
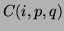 arises from the centralised moments:
arises from the centralised moments:
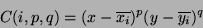 |
(14) |
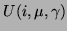 introduces velocity as:
introduces velocity as:
 |
(15) |
 is the current COM (Centre of Mass - as defined by the first order Cartesian moment) in the
is the current COM (Centre of Mass - as defined by the first order Cartesian moment) in the 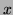 direction, while
direction, while
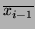 is the previous COM in the
is the previous COM in the 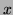 direction,
direction,
 and
and
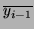 are the equivalent values for the
are the equivalent values for the 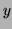 direction.
It can be seen that the equation can easily be decomposed into averaged centralised
moments (
direction.
It can be seen that the equation can easily be decomposed into averaged centralised
moments (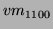 ), and then further into an averaged Cartesian moment (
), and then further into an averaged Cartesian moment (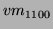 with
with
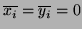 ).
The zero order velocity moments for which
).
The zero order velocity moments for which 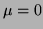 and
and 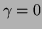 are then:
are then:
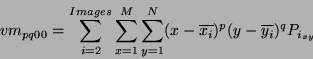 |
(16) |
which are the averaged centralised moments. The zero order components
for which 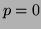 and
and 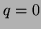 are:
are:
 |
(17) |
which is a summation of the difference between COMs of successive images (ie the velocity).
The structure of Equation 13 allows the image structure to be described together with
velocity information from both the 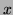 and
and 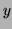 directions.
These results
are averaged by normalising with respect to the number of images and the average area of the object.
This results in pixel values for the velocity terms, where the velocity is measured in pixels per
image. The normalisation is expressed as:
directions.
These results
are averaged by normalising with respect to the number of images and the average area of the object.
This results in pixel values for the velocity terms, where the velocity is measured in pixels per
image. The normalisation is expressed as:
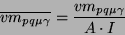 |
(18) |
where 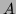 is the average area (in numbers of pixels) of the moving object,
is the average area (in numbers of pixels) of the moving object, 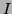 is the number of
images and
is the number of
images and
 is the normalised Cartesian velocity moment.
is the normalised Cartesian velocity moment.


Next: Zernike Velocity Moments
Up: Velocity moments
Previous: Velocity moments
Jamie Shutler
2001-09-25