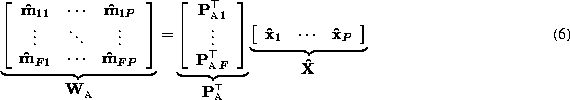
Suppose that all the cameras obey affine projections represented by (2). We write this equation with the all views and object points as follows:
The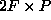 
matrix 
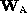is called the
measurement matrix and (6) means that
this matrix can be decomposed into a 
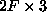matrix
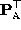representing camera motion and a
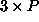matrix 
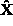representing the object shape.
This factorization can be performed through singular value decomposition
(SVD) as follows; Let
be SVD of the measurement matrix 
with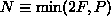 
and singular values 
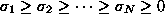. The column vectors of the 
(
)
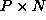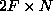matrix 
(
) are mutually orthogonal, which
means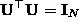 
(
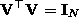). If there is no noise in the 2D
image coordinates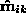 
, 
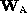is rank 3 and 
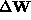in (7) is zero.
Therefore one possible factorization of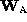 
is given by
Though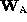 
is not necessarily rank 3 with
the presence of noise, the solution (8) is
optimal in the sense that the ``corrected'' measurement matrix
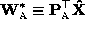minimizes a criterion
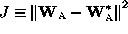under the constraint:
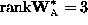[10].
However, the solution (8) is not unique; If
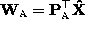is one possible factorization,
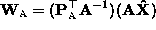yields another
factorization for arbitrary 3
3 non-singular matrix
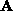. Conversely, if the measurement matrix
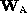is factored in two ways, i.e.
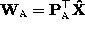and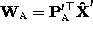 
, there exists a
3
3 non-singular matrix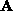 
which satisfies
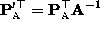and
(see appendix
A). This means that camera motion
and the object shape
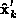obtained by decomposing the measurement matrix
differ from ``true'' values, 
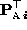and
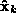, only by an unknown affine transformation
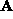, that is,
In other words, we can recover shape and motion up to an unknown affine transformation and can arbitrarily choose a 3D affine coordinate frame in terms of which structure of the motion and shape are described. We call this kind of recovery affine reconstruction.
