Noise models

Noise in imaging systems is usually either additive or multiplicative. This thesis deals only with additive noise which is zero-mean and white. White noise is spatially uncorrelated: the noise for each pixel is independent and identically distributed (iid). Common noise models are:

 

• Gaussian noise provides a good model of noise in many imaging systems [5]. Its probability density function (pdf) is:

  

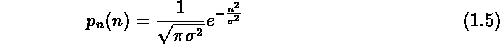
  The Gaussian distribution has an important property: to estimate the mean of a stationary Gaussian random variable, one can't do any better than the linear average. This makes Gaussian noise a worst-case scenario for nonlinear image restoration filters, in the sense that the improvement over linear filters is least for Gaussian noise. To improve on linear filtering results, nonlinear filters can exploit only the non-Gaussianity of the signal distribution.

• Laplacian noise (also called biexponential) which has this pdf:

  

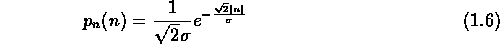
  Nonlinear estimators can provide a much more accurate estimate of the mean of a stationary Laplacian random variable than the linear average [6].

• Uniform noise is not often encountered in real-world imaging systems, but provides a useful comparison with Gaussian noise. The linear average is a comparatively poor estimator for the mean of a uniform distribution. This implies that nonlinear filters should be better at removing uniform noise than Gaussian noise. The Uniform pdf is given by:

  

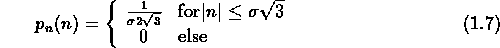
Figure 1.2 illustrates these PDFs for zero-mean, unit variance noise.

  
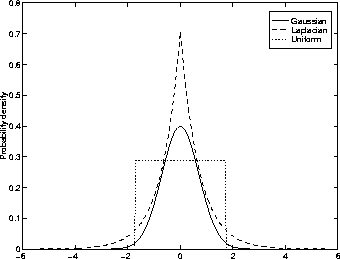
Figure 1.2: Probability density functions of the Gaussian, Laplacian and Uniform distributions