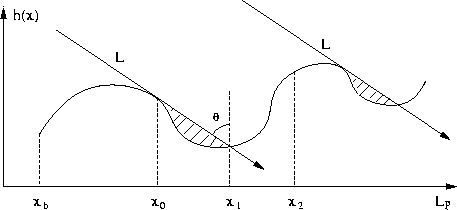
Figure 1: 2D schematic of shadowed and nonshadowed regions on a terrain-like surface. L is the lighting direction determined by the elevation angle
Yizhou Yu
Department of Computer Science
University of Illinois at Urbana-Champaign
yyz@cs.uiuc.edu

Figure 1:
2D schematic of shadowed and nonshadowed regions on a terrain-like surface.
L is the lighting direction determined by the elevation angle ![]() .
.
![]() is an occluder,
is an occluder, ![]() is on the shadow boundary caused by
is on the shadow boundary caused by ![]() ,
and
,
and ![]() is a non-shadowed point.
is a non-shadowed point.
Let us first consider recovering terrain-like height fields. For the convenience of discrete representation based on pixels, a height field is assumed to be a piecewise constant function with every pixel corresponding to a piece with constant height. Every piece of the height field is represented by the point corresponding to the center of the pixel. We also assume that the distance between the camera and the surface is sufficiently large so that the orthographic projection model is accurate. The surface is illuminated with a collimated light source which can be parameterized by a pair of polar coordinates.
Let us first check what kind of constraints are available from images
with shadows.
Let h(x) be a height field defined on a
planar domain D with a finite area in the image plane
and ![]() be the lighting direction pointing downwards with a
tilt angle
be the lighting direction pointing downwards with a
tilt angle ![]() . The normal orientation of this height field is denoted as
. The normal orientation of this height field is denoted as ![]() . The boundary
curve of domain D is
. The boundary
curve of domain D is ![]() . The projected vector of
. The projected vector of ![]() in the domain D is
in the domain D is ![]() . Let
. Let
![]() and
and ![]() be two arbitrary 2D points in D. The line segment between them is denoted as a
vector interval
be two arbitrary 2D points in D. The line segment between them is denoted as a
vector interval ![]() for convenience. Based on whether a point on the height field is in
shadow or not under lighting direction
for convenience. Based on whether a point on the height field is in
shadow or not under lighting direction ![]() , there are two different sets of constraints
(Fig. 1).
, there are two different sets of constraints
(Fig. 1).
Let us first focus on how to represent the inequality constraints (1) and (4) in a graph [5].

A shadow graph can be induced from an image of the height field under an arbitrary lighting
direction ![]() . Shadowed pixels can be detected from the image, and an occluder can be located
for each continuous shadow segment with the knowledge of the lighting direction. For example, if
. Shadowed pixels can be detected from the image, and an occluder can be located
for each continuous shadow segment with the knowledge of the lighting direction. For example, if
![]() is a shadow segment and the vector from
is a shadow segment and the vector from ![]() to
to
![]() is in the direction of
the projected lighting direction
is in the direction of
the projected lighting direction ![]() , the point at
, the point at ![]() is the occluder of all the points in
is the occluder of all the points in
![]() . There should be an edge
. There should be an edge ![]() with weight
with weight ![]() in the induced graph for all
in the induced graph for all ![]() . This graph basically encodes the shadow
constraints available from the image. All the edge weights in this graph should be positive.
However, this graph can have negative weights if the additional antishadow
constraints in Eq. (4) are represented as well.
. This graph basically encodes the shadow
constraints available from the image. All the edge weights in this graph should be positive.
However, this graph can have negative weights if the additional antishadow
constraints in Eq. (4) are represented as well.
Suppose we have multiple images of the height field under a set of lighting directions
![]() . Each of the images has its own shadow graph. Finally, the edges from all of
these individual graphs can be accumulated into one graph that is corresponding to all the
images.
. Each of the images has its own shadow graph. Finally, the edges from all of
these individual graphs can be accumulated into one graph that is corresponding to all the
images.
![]()
Proof
Suppose there is a circular path in the graph and a node v is on the path. Since all the
arcs on this path have positive weights, it is easy to conclude that h(v) > h(v) by starting from
v, going through this path and back to v. A contradiction.
When dealing with real images with noise, shadow detection cannot be expected to be error free. Inaccurate shadow segmentations may result in cycles in the induced shadow graphs. Since cycles can lead to the above contradiction, we must convert a cyclic graph into an acyclic one by removing some of the edges in the graph [5].

There are a set of nodes ![]() in
in ![]() that do not have any incident edges with
positive weights, which means they are not shadowed by any other points in any of the images.
The highest point(s) of the height field surely belongs to this set because there is no other points
which can occlude it(them) from the light sources. The absolute height values of
the nodes in
that do not have any incident edges with
positive weights, which means they are not shadowed by any other points in any of the images.
The highest point(s) of the height field surely belongs to this set because there is no other points
which can occlude it(them) from the light sources. The absolute height values of
the nodes in ![]() are unrecoverable from shadow constraints. However, if we can recover their
height values from other approaches such as stereo, the information embedded in
are unrecoverable from shadow constraints. However, if we can recover their
height values from other approaches such as stereo, the information embedded in
![]() can be used for obtaining an upper bound of the height at any point in
can be used for obtaining an upper bound of the height at any point in ![]() . The set of
edges in
. The set of
edges in ![]() connecting
connecting ![]() and
and ![]() becomes the most important for this purpose.
Suppose there is a node
becomes the most important for this purpose.
Suppose there is a node ![]() and a set of associated edges
and a set of associated edges ![]() such
that if an edge
such
that if an edge ![]() ,
, ![]() . The upper bound of the height
at the point corresponding to node v can be obtained from
. The upper bound of the height
at the point corresponding to node v can be obtained from
![]()

Figure 2: A surface reconstruction example from [5].
(a) Input images for a plaster material sample
lit from eight lighting directions;
(b) a synthetic image of the recovered height field illuminated from
the same lighting direction as in the first input image;
(c) a synthetic image of the recovered height field illuminated from
a novel lighting direction.
Let us exam the asymptotic behavior of this upper bound when we increase the number
of input images with lighting directions covering the whole lighting hemisphere. The set ![]() will shrink and approach its limit which is the set of the highest points of the height field.
Otherwise, assume there is a pair of nodes
will shrink and approach its limit which is the set of the highest points of the height field.
Otherwise, assume there is a pair of nodes ![]() and
and ![]() . We can always
design a lighting direction from which the point corresponding to
. We can always
design a lighting direction from which the point corresponding to ![]() shadows the point
corresponding to
shadows the point
corresponding to ![]() , which means
, which means ![]() , a contradiction. Since eventually
, a contradiction. Since eventually ![]() only has nodes at the same height, we do not need to seek their relative height through other
reconstruction techniques. Our interest should be focused on the relative height of other points
compared to the highest points whose height can always be set to zero.
only has nodes at the same height, we do not need to seek their relative height through other
reconstruction techniques. Our interest should be focused on the relative height of other points
compared to the highest points whose height can always be set to zero.
See proof in [5].
It is clear that the antishadow constraints can be derived from the shadow constraints if we have a very dense set of images since the height field itself can be recovered from the shadow constraints alone according to the above Proposition. However, if we only have a sparse set of images, this is not necessarily true. Representing these antishadow constraints in a shadow graph usually can provide additional information. According to Eq. (4), antishadow constraints transform to additional edges with negative weights. Cycles can appear in the resulting graph. However, the accumulated weight of any cycle can not be positive according to the following Proposition.
![]()
The transitive closure of a shadow graph G with cycles is still well-defined because negative
cycles do not interfere with the objective to seek paths with maximum accumulated weights
according to the definition. The resulting graph ![]() can still be used for obtaining an upper
bound of the height for any point in
can still be used for obtaining an upper
bound of the height for any point in ![]() . Since there may be negative edges pointing from
nodes in
. Since there may be negative edges pointing from
nodes in ![]() to some nodes in
to some nodes in ![]() , these edges can be used for obtaining a lower bound
for some nodes in
, these edges can be used for obtaining a lower bound
for some nodes in ![]() . Since it is not guaranteed that there is an edge from each node in
. Since it is not guaranteed that there is an edge from each node in
![]() to some node in
to some node in ![]() given a sparse set of images, we can only obtain lower bounds
for a subset of nodes in
given a sparse set of images, we can only obtain lower bounds
for a subset of nodes in ![]() . And these lower bounds may appear useful in combination with
other surface reconstruction techniques.
. And these lower bounds may appear useful in combination with
other surface reconstruction techniques.
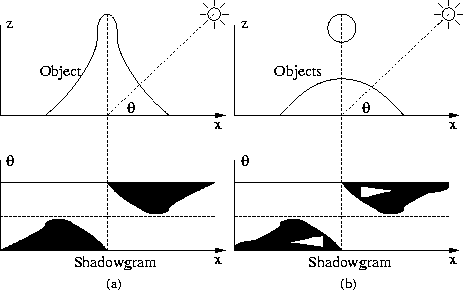
Figure 3:
(a) A shadowgram for a one-dimensional terrain-like surface;
(b) a shadowgram for a one-dimensional non terrain-like surface.
Shadow information can also be described using another representation known
as a Shadowgram [3, 1]. Let us first look at shadowgrams
for a one-dimensional terrain-like surface illuminated by a collimated
light source parameterized by a single angle ![]() . As shown in
Fig. 3, the shadowgram is a binary function defined on
the angle,
. As shown in
Fig. 3, the shadowgram is a binary function defined on
the angle, ![]() , and the spatial dimension of the terrain, x.
A white entry in the shadowgram indicates that image pixel x was lit
when the light source was at angle
, and the spatial dimension of the terrain, x.
A white entry in the shadowgram indicates that image pixel x was lit
when the light source was at angle ![]() , while a black entry indicates
that it was shadowed. It was shown in [3] that the shadowgram
generated by a terrain-like surface can be completely described by two
curves bounding the black regions:
, while a black entry indicates
that it was shadowed. It was shown in [3] that the shadowgram
generated by a terrain-like surface can be completely described by two
curves bounding the black regions: ![]() and
and ![]() .
For a specific point x,
.
For a specific point x, ![]() and
and ![]() represent the
lighting angles at which x is lit for the first and last time, respectively.
Therefore,
represent the
lighting angles at which x is lit for the first and last time, respectively.
Therefore, ![]() .
If the light source travels from horizon to horizon, it is possible that one
of these angles might be equal to 0 or
.
If the light source travels from horizon to horizon, it is possible that one
of these angles might be equal to 0 or ![]() .
.
![]() unless the point in question is a global
maximum of the scene. Because one has this guarantee, it is possible to
reconstruct the surface by integrating
unless the point in question is a global
maximum of the scene. Because one has this guarantee, it is possible to
reconstruct the surface by integrating ![]() and
and ![]() .
.
When the one-dimensional surface is non terrain-like,
the shadowgram possesses not only
two curves, but also some white holes where one would expect darkness
if the surface were a terrain. Here ![]() and
and ![]() are not defined as first and last lighting curves, but rather as the
envelope of the shadowgram which lies closest to the middle horizontal
line defined by
are not defined as first and last lighting curves, but rather as the
envelope of the shadowgram which lies closest to the middle horizontal
line defined by ![]() . It is shown in [4] that
using these two curves to reconstruct the surface will produce the
surface's generated terrain which is defined to be its upper envelope.
Furthermore, the holes in the shadowgram may be used to carve pieces
out of the generated terrain for reconstructing some of the hidden
parts of the surface.
. It is shown in [4] that
using these two curves to reconstruct the surface will produce the
surface's generated terrain which is defined to be its upper envelope.
Furthermore, the holes in the shadowgram may be used to carve pieces
out of the generated terrain for reconstructing some of the hidden
parts of the surface.
In a general situation, a surface in a 3D space is parameterized by two variables, and the lighting direction is defined by two angles. The shadowgram thus becomes a four-dimensional function defined on all these four variables. It becomes so complicated that often three dimensional cross sections are investigated [1].
If there are additional assumptions on the smoothness of the surface (e.g. it is twice differentiable), one may find that it is possible to reconstruct a spline approximation of the original surface from shadow constraints available at a sparse set of locations [2]. The normal constraint in Eq.(3), which has not been made use of so far, becomes important in spline surface reconstruction.