The notation of pixel connectivity describes a relation between two or more pixels. For two pixels to be connected they have to fulfill certain conditions on the pixel brightness and spatial adjacency.
First, in order for two pixels to be considered connected, their pixel values must both be from the same set of values V. For a grayscale image, V might be any range of graylevels, e.g. V={22,23,...40}, for a binary image we simple have V={1}.
To formulate the adjacency criterion for connectivity, we first introduce the notation of neighborhood. For a pixel p with the coordinates (x,y) the set of pixels given by:
is called its 4-neighbors. Its 8-neighbors are defined as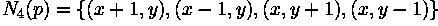
From this we can infer the definition for 4- and 8-connectivity: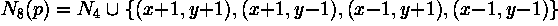
Two pixels p and q, both having values from a set V are 4-connected if q is from the set 
and 8-connected if q is from 
.
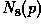General connectivity can either be based on 4- or 8-connectivity; for the following discussion we use 4-connectivity.
A pixel p is connected to a pixel q if p is 4-connected to q or if p is 4-connected to a third pixel which itself is connected to q. Or, in other words, two pixels q and p are connected if there is a path from p and q on which each pixel is 4-connected to the next one.
A set of pixels in an image which are all connected to each other is called a connected component. Finding all connected components in an image and marking each of them with a distinctive label is called connected component labeling.
An example of a binary image with two connected components which are based on 4-connectivity can be seen in Figure 1. If the connectivity were based on 8-neighbors, the two connected components would merge into one.
Figure 1 Two connected components based on 4-connectivity.
©2003 R. Fisher, S. Perkins,
A. Walker and E. Wolfart.
