Theory of Surface Clusters

The goal of the surface cluster formation process is to isolate the visible portion of each distinct three dimensional object's surface, so that later stages of the scene analysis can associate a model with the surface cluster.

The primary input into the process is the set of surface hypotheses produced as output of the processes described in Chapter 4. The surface hypotheses are linked by adjacency, and relative surface orientation at the boundaries is known.

The output of the process is a set of surface clusters hierarchically linked by inclusion, with each consisting of a set of surface patches. Though the surface cluster is not closed (i.e. it is missing the back side), it defines a solid bounded in front by the visible surfaces.

The surface cluster formation process is closely linked to the model structure known as the ASSEMBLY, which is defined in Chapter 7. The ASSEMBLY is a model of a three dimensional solid and is composed of SURFACEs or recursively defined subcomponents. Properties we would like the surface cluster formation process to have are:

• Every model ASSEMBLY is wholly contained in at least one surface cluster.
• There are surface clusters containing only a single primitive model ASSEMBLY.
• Only complete ASSEMBLYs are contained in surface clusters.
• There is a hierarchy of surface clusters corresponding to the hierarchy of model ASSEMBLYs.

However, at this stage of image analysis, models are not available to help segment the image, nor is the model base known. Hence, to achieve our goal with these properties, two assumptions must be made about the model structure independent of the actual models:

• If a set of model SURFACEs is completely surrounded by a set of concave or crack surface boundaries, then they are modeled as a distinct ASSEMBLY.
• If two model SURFACEs are adjacent across a convex surface boundary, then they are in the same model ASSEMBLY.

For example, a nose on a face, or a handle on a coffee cup would thus be in separate ASSEMBLYs.

The process of creating the surface clusters has three steps:

1. Classify adjacent surface regions as connected or unconnected.
2. Form primitive surface clusters from connected groups of surfaces. (Primitive surface clusters are those that cannot be split further.)
3. Merge primitive surface clusters to form larger surface clusters.

These steps are described in detail below.

The algorithm is conservative, in that it tries to avoid splitting the smallest model ASSEMBLYs between surface clusters at the price of creating clusters containing several ASSEMBLYs. Splitting an object between several different surface clusters would be catastrophic because it asserts that the segregated components are unrelated. Creating clusters larger than single objects is mainly an annoyance, because the rest of the recognition process then has more work to identify the objects.

Determining Surface Connectivity

The segmented surface image can be thought of as a graph, where the nodes of the graph represent the surface patches and the arcs of the graph represent surface adjacency. These arcs will be labeled as connecting or segmenting, according to criteria based on boundary type and configuration. The connection criteria are simple and logical, except for a laminar surface case (described shortly) and are based on obvious three dimensional properties of surface connectivity and object depth ordering. Splitting the graph at segmenting boundaries partitions the scene into sets of connected surfaces - forming the primitive surface clusters.

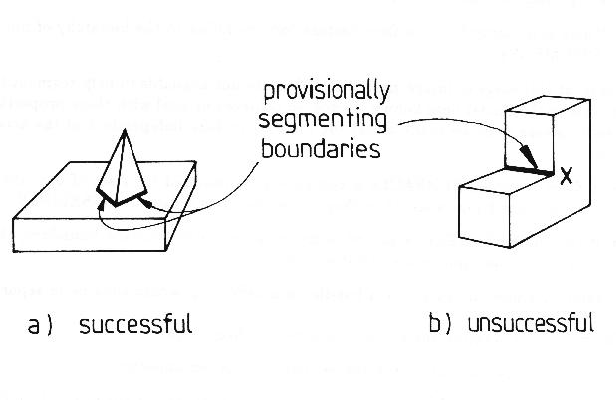
We assume that the modeled objects are segmented into subcomponents at chains of connected concave boundaries. As concave model boundaries are observed as concave image boundaries, the latter are potentially segmenting. In Figure 5.1 part (a), the concave boundary is truly segmenting.

Further, distinct objects are often on opposite sides of concave surface orientation boundaries. For example, a block sitting on a table has concave boundaries isolating it from the table. Nameable subcomponents of natural objects often fit flushly with concave boundaries, as in the nose-to-face junction. Because the boundary is concave, it is indeterminate whether the two surfaces are joined or merely in contact. Moreover, it is usually impossible to tell which surface passes underneath the other past the point of the observed concave boundary. So, the conservative approach suggests that this boundary causes a segmenting arc. Assuming concave boundaries necessarily imply segmentation leads to contradictions as seen in Figure 5.1 part (b), where there is no reasonable shape boundary at point X to continue segmentation. If there are other connections between the two surfaces that do not involve a segmenting boundary, then the final surface cluster will include both surfaces.

Figure 5.1: Concave Boundaries Provisionally Segment

A more complicated case occurs with crack-type boundaries. Here, two surfaces may be coincidentally aligned, or part of a flush contact boundary (as often occurs with revolute joints). Because of the ambiguity, it is assumed that connectivity does not hold across crack-type joints.

Whenever one object sits in front of or on top of another, the intervening boundary is always either concave or obscuring, as illustrated in Figure 5.2. To complete the isolation of the cylinder in part (a) from the background plane, a rule is needed to handle obscuring boundaries. As these usually give no clues to the relation between opposing surfaces (other than being depth separated), surfaces will usually be segmented across these, and so segmenting arcs join the nodes representing these surfaces.

Figure 5.2: Object Ordering Causes Concave and Obscuring Boundaries

Connectivity holds across some obscuring boundaries. Disregarding coincidental alignments, the one exception found occurs when laminar objects fold back on themselves, as illustrated in Figure 5.3. This figure shows a leaf folded over and the two surfaces of a trash can. The arrows on the boundary mean that it is an obscuring type boundary with (here) the front surface lying to the left when looking along the boundary in the direction of the arrow. In both cases, the two surfaces are connected, even though an obscuring boundary intervenes, and so here a connecting arc is used. Fortunately, this case has a distinctive signature: the arrow vertices shown at the right side of the figure are paradigmatic of the junction formed by a folding laminar surface. Viewpoint analysis (by octant) shows that these are the only special trihedral vertex label cases needed for two connected laminar surfaces. Curved laminar surfaces are (here) treated locally as two connecting planar laminar surfaces.

Figure 5.3: Connectivity Holds Across Some Obscuring Boundaries

Two surfaces lying on opposite sides of convex boundaries ordinarily belong to the same object, though coincidental alignment may also produce this effect. Hence, surfaces on opposite sides of convex boundaries cause connecting arcs. A surface orientation boundary that is both concave and convex in places is broken up by the curve segmentation assumptions. To summarize, the constraints that specify the connectivity of surface patches are:

• Connectivity holds across convex shape boundaries.
• Connectivity does not hold across concave and crack shape boundaries.
• Connectivity does not hold across obscuring boundaries, except when the boundaries are configured as in Figure 5.3.

Forming Primitive Surface Clusters

Primitive surface clusters are formed by collecting all surface patch nodes that are directly or transitively connected in the graph, once all arcs are labeled as "segmenting" or "connecting". Thus, image features that can only belong to the same object lie in the same surface cluster, and features that possibly belong to other objects do not lie in the cluster.

Depth Merged Surface Clusters

The goal of the surface cluster process is to associate all components of an object in some surface cluster. All components of a model may not occur in the same primitive surface cluster for several reasons:

• The object may consist of several subcomponents, each of which appears in smaller surface clusters.
• The object may fold back on itself, and thus be observed as two different components separated by an obscuring boundary.

In the test image, the upper and lower robot arms lie in separate primitive surface clusters, but the model ASSEMBLY joining them does not yet have a surface cluster. Depth merged surface clusters are intended to provide the context for complete objects.

This merging process is constrained by the following observation, referring to Figure 5.4. If there are four surface clusters (A, B, C, and D), an object might be wholly contained in only one of these, but it might also obscure itself and be in more than one. Hence, reasonable groupings of surface clusters containing whole objects are AB, AD, BC, BD, CD, ABC, ABD, ACD, BCD and ABCD. AC is an unlikely grouping because there is no obvious relation between them.

Figure 5.4: Depth Merging Example

Merging all surfaces behind a given surface does not solve the problem. If only surfaces ABC were present in the above scene, then merging behind does not produce a containing surface cluster if the true object was ABC. Similarly, the technique of merging all surfaces in front fails if both the object and grouping were ACD. Neither of these processes individually produce the correct clusters. To avoid this problem, a more combinatorial solution was adopted.

Before the computational constraints for depth merging are given, one refinement is necessary. Rather than considering depth merging for all surface clusters, certain sets of surface clusters can be initially grouped into equivalent depth surface clusters. These occur when either surface clusters mutually obscure each other, or when there is no obvious depth relationship (e.g. they lie across a concave surface boundary). An example of where two surface clusters mutually obscure is with the robot lower arm and trash can surface clusters in the test image. When these cases occur, all such primitive surface clusters can be merged into a single equivalent depth surface cluster. Thereafter, the combinatorial depth merging process only considers the equivalent depth surface clusters.

The properties defining the equivalent depth clusters are:

Let:

{$P_1, ... P_n$}	be the primitive surface clusters
front($P_i,P_j$)	means $P_i$ is in front of $P_j$, which holds if there is a
	surface in $P_i$ with an obscuring relation to a surface in $P_j$
beside($P_i,P_j$)	means $P_i$ is beside $P_j$, which holds if there is a surface
	in $P_i$ that shares a concave or crack boundary with a surface in $P_j$
{$E_1, ... E_m$}	be the equivalent depth clusters
$E_i$	= { $P_{i1}, ... P_{is}$}

Then, the relationship between the $P_i$ and the $E_i$ is defined by:

(1) If $\mid E_i \mid$ $\not=$ 1, for any $P_{ia}$ $\in$ $E_i$, there is a $P_{ib}$ $\in$ $E_i$ such that:
	front($P_{ia}$,$P_{ib}$) and front($P_{ib}$,$P_{ia}$)
		or
	beside($P_{ia}$,$P_{ib}$)
(2) If $\mid E_i \mid$ $=$ 1 and $E_i$ = { $P_i$ }, then for all $P_j$ $\not=$ $P_i$
	not front($P_i$,$P_j$) or not front($P_j$,$P_i$)
		and
	not beside($P_i$,$P_j$)
(3) The $E_i$ are maximal (i.e. no $E_i$ contains another $E_j$).

Equivalent depth surface clusters that only contain a single primitive surface cluster are replaced by that primitive surface cluster (for compactness).

Then, using the same definitions, the depth merged surface clusters are sets of equivalent depth surface clusters:

Let:
	efront($E_i$,$E_j$)	mean equivalent depth surface cluster $E_i$ is in front of
		equivalent depth surface cluster $E_j$, which occurs if there are
		primitive surface clusters $P_{ia}$ $\in$ $E_i$ and $P_{jb}$ $\in$ $E_j$ such that front($P_{ia}$,$P_{jb}$)
	linked($E_i$,$E_j$)	holds if efront($E_i$,$E_j$) or efront($E_j$,$E_i$)
	{$D_1, ... D_n$} be the depth merged clusters
	$D_i$ = { $E_{i1}, ... E_{it}$}
Then:
	the $D_i$ are all subsets of {$E_1, ... E_m$} such that for any $E_{ia}$ $\in$ $D_i$
		there is a $E_{ib}$ $\in$ $D_i$ satisfying linked($E_{ia}$,$E_{ib}$)

The implementation of these definitions is straightforward and leads first to the construction of primitive surface clusters, then to formation of equivalent depth clusters and finally to the linking of these into larger depth merged surface clusters. The background and picture frame surfaces are omitted.

The surface clusters are linked into the image description graph started in Chapter 3 by the following additions:

1. Every surface cluster node is linked to a set of surface hypotheses.
2. Surface clusters are linked into a hierarchy by containment.
3. Surface clusters are linked to chains of boundary elements that surround them.