 |
Based on the experience of this and more recent research, the SMS object representation system [70] was designed. Extensions over the geometric model approach described above include: multiple, alternative representations (curve, surface or first and second-order volumetric primitives), surfaces that extend around the objects, and can have holes, key feature models, parameterized feature sizes and properties (e.g. surface curvatures), unconstrained degrees-of-freedom in reference frame transformations, multiple levels of scale-based representation and viewpoint dependent visibility information.
The goal of SMS is to represent the visual aspects of an object that characterize its identity, rather than describe its shape. Hence, the modeling approach aims to provide representations that closely correspond to reliably extractable image features. This implies that:
The SMS structural models are linked by a subcomponent hierarchy similar to that described for IMAGINE I, where subcomponents can be joined to form larger models by reference frame transformations. SMS allows partially constrained relationships, either through the use of variable parameters in the transformation, or by use of an unconstrained degree-of-freedom relationship that, for example, aligns a subcomponent axis vector with a given vector direction in the main model.
The primitive ASSEMBLY structure (i.e. one without subcomponent ASSEMBLYs) can have three non-exclusive representations based on curve, surface or volumetric primitives. The main motivation for the structural alternatives is that different sensors produce different data features (e.g. stereo produces good edge features, ranging produces good surface features and bodyscanners produce good volumetric features). SMS allows one to use the same model to interpret data from all of these scenes; whether this is useful is not known yet.
The curve representations are piecewise circular, elliptic and straight arcs, segmented by the curvature discontinuity criteria proposed in Chapter 3. Surface patches are similar to those described above, except that SURFACEs can now be connected on all sides (e.g. a complete cylinder instead of two arbitrarily segmented patches) and may have holes. Patches are carved out of infinite planes, cylinders and cones, or (finite) tori. Volumetric primitives are based on those proposed by Shapiro et al. [146]. They used a rough three dimensional object model based on sticks (one primary dimension of extension), plates (two dimensions) and blobs (three dimensions) and structural interrelationships. This approach allowed development of more stable relational models, while still symbolically characterizing object structure. The SMS modeling system also has some second-order volumetric representations [73] for small positive features (bump, ridge, fin and spike) and negative features (dent, groove, slot and hole). The volumetric primitives provide model primitives that can be matched to rough spatial characterizations of the scene - such as when stereo provides only a sparse depth image.
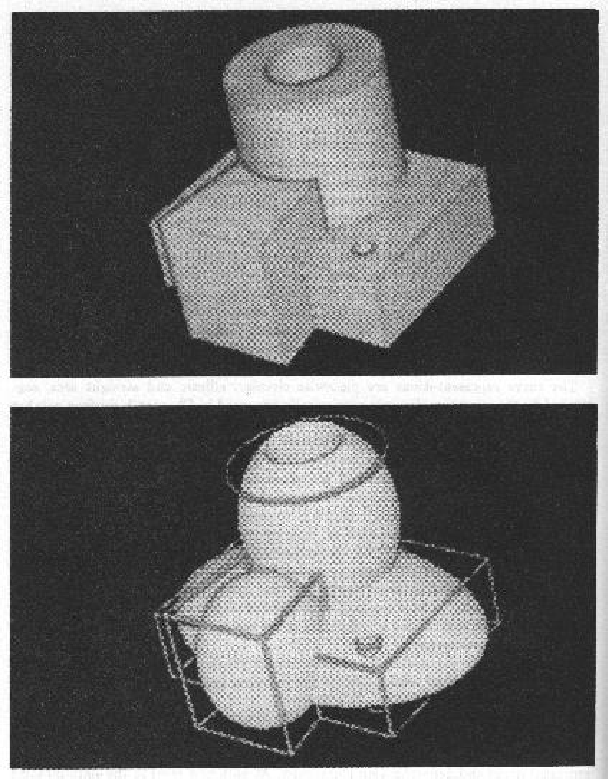
In Figure 7.9 we can see first a surface characterization of a "widget" and then a volume and curve based model. Each representation approach captures the "feel" of the object differently.
There is a simplification hierarchy in SMS, which links together models through scale relationships. This development is more speculative, and tries to fuse the ideas of Marr and Nishihara [111] and Brooks [42] on scale-based refinement of model representations and generalization hierarchies. At each new level in the simplification hierarchy, models have their features simplified or removed, resulting in broader classes of objects recognizable with the model. Figure 7.10 shows a coarse and fine scale model of an ashtray (which is also considerably more free-form than the "widget"). The main difference between the two representations is the simplification of the cigarette rest corrugations in the fine scale model to a plane in the coarse model. The plane is a suitable representation for when the object is too distant from the observer to resolve the fine detail.
Following ACRONYM [42], all numerical values can be symbolic variables or expressions, as well as constants. This has been used for generic model representation, by allowing size variation amongst the recognizable objects. Variables are defined as either local or global to a model and are bound by a dynamic scoping mechanism. For example, one could define a robot finger with an external scale parameter and an internal joint angle parameter. When defining a robot hand using several instances of the fingers, than each finger would have its own joint position, but all fingers would have the same scale parameter. Figure 7.11 shows the ashtray with parameter changes causing a wider and deeper shape.
Besides the structural model, each SMS model has a set of constraints and descriptions. Some constraints are expressed in algebraic form, following ACRONYM, and affect the model variables (e.g. feature sizes and joint angles). These constraints can be exploited in the simplification hierarchy, as in ACRONYM. Evidence constraints bound properties such as area, curvature or relative position. These are used primarily for model invocation, as discussed here. in Section 7.2. Finally, relations between the volumetric primitives can be given [146], such as "a STICK touches a PLATE".
Each SMS model has some visibility information directly represented along with the object-centered information described above. While this information is derivable from the geometric model, in principle, experience with IMAGINE I showed that these derivations were time-consuming, because a full raycast image was synthesized and then analyzed. (Chapter 9 elaborates on this).
The visibility information is organized into visibility groups, where each group corresponds to a different topological viewpoint of the immediate subcomponents. While this is still an open research problem, our work suggests that the complexity of the viewsphere [104] of a complicated object, can be reduced by (1) only considering occlusion relationships between immediate subcomponents of a model, thus creating a hierarchy of viewspheres, and (2) only considering large scale relationships, like surface ordering. Each visibility group records which subcomponents are visible or tangential (i.e. possibly visible) and for the visible ones, which are partially obscured. New viewpoint dependent features are also recorded, such as surface relative depth ordering, TEE junctions and extremal boundaries on curved surfaces. Each viewpoint has a set of algebraic constraints that specify the range of object positions over which the given viewpoint is visible.
As can be seen, the SMS models are considerably richer than those used for IMAGINE I, and form the basis for the IMAGINE II system currently being developed (see Chapter 11). The rest of this book describes the results obtained using the IMAGINE I models.