 |
Models are invoked by attributes suggesting objects; thus invocation is necessarily coincidental. Hypothesis construction is more constraining, requiring geometric coordination among features as dictated by the model, but can still leave spurious, well advanced, hypotheses that need to be eliminated. Hence:
verification aims to ensure that what is recognized is only what is contained in the scene.
In a philosophical sense, verification should try to maximally confirm the validity of the hypothesized identity of an image structure, to the limits of the object representation. The point is to ensure that the object both physically exists and has the requisite properties, by extending the depth of the subordinate concept structure beyond merely superficial attributes. In a sense, this is a true "seeing" of the object. Previous stages of analysis only considered subsets of the features in a "suggestive" sense, whereas verification should now look for all features and can report what it finds.
More practically, verification should also eliminate hypotheses that arise from coincidental arrangements of image features. This approach leads to defining a set of constraints that an object must satisfy to be said to exist and have a given identity. These, in turn, entail knowing both what is important in an object and its representation, and what makes it appear as it does.
We would like reasonable criteria for ensuring correct object
hypotheses, with "reasonable" encompassing both richness of detail
and conceptual appropriateness.
Unfortunately, "ensuring" is
impossible because all interpretations of sensory data are necessarily
imperfect and because no real object can be completely and uniquely characterized.
Practical problems are related and stem from impoverished models and descriptive terms
and lack of resolution in the data.
However, some verification is both necessary and of value and
should remove the most obvious cases of misidentification.
Existence Verification
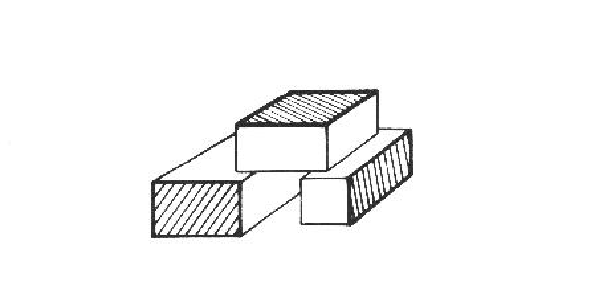
Little work has addressed the question of: "Does the object exist, or are the features merely coincidental?". Geometric constraints increase the certainty by showing that the image features are consistent with a particular object instance, but they do not guarantee that the features are causally related. Figure 10.1 shows three orthogonal planes that invoke a cube model, but fail to meet the general physical requirements of connectedness. Hence, we can help ensure existence by requiring the objects to be completely bounded by a connected set of surfaces.
Because of philosophical and practical difficulties, the work will only
consider how to eliminate ASSEMBLYs whose features are definitely unrelated.
Identity Verification
Identity verification is needed because similar models could be invoked and successfully constructed. This suggestive "recognition" is appropriate for artistic vision systems, but inappropriate for precise object recognition, which is the intent of this research.
Verification could be achieved by synthesizing an image from the model and then doing detailed surface comparisons, but this is both computationally expensive and unnecessary. Considering all object features would be ideal for verifying identity. Unfortunately, practicality and finite termination requires using only a limited subset of all possible properties. Verification should be carried out at a conceptual level that is efficacious, representationally appropriate, and efficient. As this research has concentrated on object shape, our verifying properties are based on shape and structural relationships. Further, as the data is already segmented, we will use the segments themselves (as compared to the raw data).
Our segmentation assumptions imply that surface class, curvature parameters and boundary location define the surfaces (though they do not distinguish subtle differences in shape). Comparison requires knowing the surface's three dimensional position and which observed boundaries correspond to model boundaries (as distinct from obscuring or extremal boundaries). However, as position estimates may be slightly erroneous and segmentation boundaries may not be precisely placed (as at curvature discontinuities), detailed boundary and surface comparison is inappropriate.
For ASSEMBLYs, identity is maximally verified if all the predicted visible features are found in the correct places. The subcomponent identities and their relative geometric positions were verified previously by the hypothesis construction process. Hence, to increase our certainty, we must check that their observed interrelationships (e.g. adjacencies, self-occlusions) correspond to those predicted by the model.
The hypothesis construction process understands occlusion and records missing structures whose locations were predicted, but which were declared obscured based on other evidence. Verification of partially obscured structures must show that the remaining visible portions of the object are consistent with what is predicted given the model, its spatial location, the occlusion annotations and the image evidence.
As certainty of identity is impossible, the goal of identity verification is to falsify hypotheses that do not satisfy all identity constraints.
In summary, verification must: