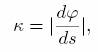
Measure Curvature Variation

Curvatures of surfaces are very important in computer vision because they are the key to compute shape descriptors and to classify different classes of surfaces. From geometric point of view, there are two important types of curvature: extrinsic curvature and intrinsic curvature. The extrinsic curvature of curves in two- and three-space was the first type of curvature to be studied historically, culminating in the Frenet formulas, which describe a space curve entirely in terms of its "curvature," torsion, and the initial starting point and direction. (more information)

In computer vision we usually have an 2D image input. Geometrically in the plane, the situation is clear. If φ is the angle between the tangent line and the x-axis then the one defines the curvature to be

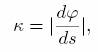
where s is arc length. (I.e. s measures distance as one travels along the curve.)

By the chain  rule,                         . Now write                 . Then

Thus to fine the curvature, it suffices to find         and to find ν.

Clearly                     .

 If one remembers the formula for arc-length, one can then anticipate that

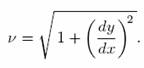
The intuitive significant of ν is that it is the speed at which a point travels along the curve when its x coordinate increases at a rate of one unit/second. (Thus the formula

says that in order to compute distance one integrates speed.)

Since φ is the angle between the direction in which the point on the curve is moving and the direction of te x-axis (i.e. horizontal), one can see that ν=secφ. Since tanφ is the slope of he curve i.e. tanφ = dy/dx, we get

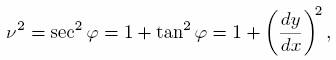
which is essentially the formula for ν anticipated above.

An alternate explanation is to derive the formula ν = secφ by starting with the standard formula for the arc length,

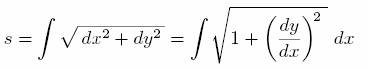
to see that

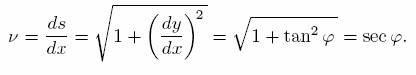
(Note that φ is by definition an acute angle, so secφ≥0.)

The formula for the curvature of the graph of a a function in the plane is now easy to obtain. Since φ is the angle of the tangent line, one knows that tanφ is the slope the curve at a given point, i.e

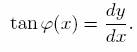
Differentiating with respect to x yields (by the chain rule)

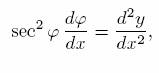
and so

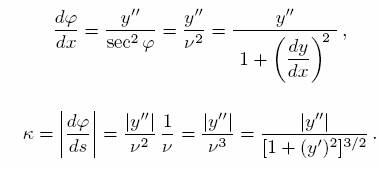
Example

Obviously the above method can be implemented with various different ways. The best algorithm known so far is that presented in On Curvative Estimation of ISO Surfaces in 3D Gray-Value Images and the Computation of Shape Descriptors [PDF] which apart from being successfully applied to curvatures of edges in 3d images, it is also successful in cases that older algorithms failed like curved plates, hollow objects and concentric shells.

Bibliography

E.L.Lady Handout on curvatives, University of Hawaii

Bernd Bieger, Frederik J Timmermans Lucas J. van Viet, On Curvative Estimation of ISO Surfaces in 3D Gray-Value Images and the Computation of Shape Descriptors, IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE, VOL. 26, NO. 8, AUGUST 2004.

Website

mathworld.wolfram.com