The Trilinear Tensor
The trilinear tensor captures the geometry of three images.
It is known that the trilinear tensor of three images is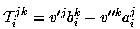 
,
where 
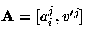
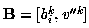denote
the 3x4 camera matrices from the first image to the second and third
images, respectively.
The tensor acts on a triplet of matching point p,p',p''
in the following way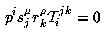 
,
where s are any two lines passing through the point p'
and r are any two lines passing through the
point p''. If s,r stand for the canonical
horizontal and vertical lines, then in standard notation we obtain the
following
four equalities, referred to as "trilinearities"
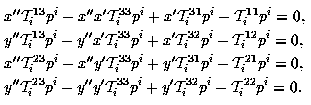
Figure
The trilinear tensor is the meeting of a ray and two planes.
The planes are passing through the matching points in the second and
third images, respectively.
Different lines in the image plane define the orientation of the planes.
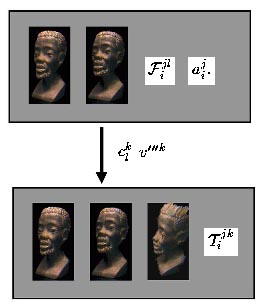
Tensor Operators
Tensor operators modify the tensor coefficients to reflect the motion
of the one of the three cameras. Let 
denote the initial tensor of
the two reference images
and let 
stand for the rotation matrix
between them. Now assume one wishs to move the second image
by the rotation matrix 
and translation vector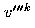 
,
then the new
tensor will be:
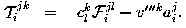
We use the tensor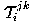 
to
reproject the novel image.
The Algorithm
At pre-processing we perform the following steps
For each novel image we perform the following steps:
-
Accept the rotation
and translation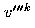
of the novel image.
-
Construct the new tensor
-
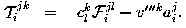
Reproject the novel image.
Trilinear tensor of the two
images
We show elsewhere that when the third image coincide with the second
image, then the
trilinear tensor collapses into the fundamental matrix.
As a result, in every place we use a tensor we can use either the fundamental
matrix (in its tensor form)
or the usuall trilinear tensor.
Rotation Matrix from The Trilinear Tensor
We show elsewhere that the rotation matrix can be recovered directly
from the trilinear tensor without
recovering the epipole first.
Reprojection with the trilinear
tensor
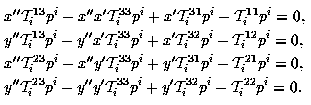
The trilinearities can be used to recover the third image - (x",y")
if the tensor is known and
we are given a pair of matching points in the first two images. This
is the key to reprojection
using the trilinear tensor.
Example
On the left are a pair of images captured with an indycam.
On the right is a generated image.
Contact
The paper "Novel view Synthesis in Tensor Space" by Shai
Avidan & Amnon Shashua, appeared in CVPR97.
Retrieve a gziped postscript copy here.
Visit us at:
Shai Avidan
Dr. Amnon Shashua
For comments please e-mail: avidan@cs.huji.ac.il