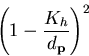Next: Defocus Blur of a
Up: No Title
Previous: Hyperboloidal Mirrors
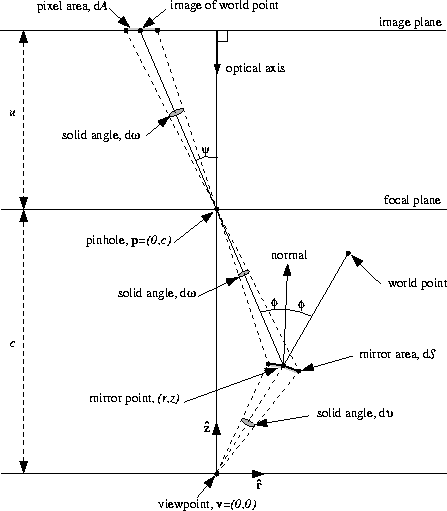
In this section, we assume that the conventional camera used
in the catadioptric sensor has a frontal image plane located at a
distance u from the pinhole, and that the optical axis of the
camera is aligned with the axis of symmetry of the mirror. See
Figure 8 for an illustration of this scenario.
Then, the definition of resolution which we will use is the following.
Consider an infinitesimal area  on the image plane.
If this infinitesimal pixel images an infinitesimal solid angle
on the image plane.
If this infinitesimal pixel images an infinitesimal solid angle
 of the world, the resolution of the sensor
as a function of the point on the image plane at the center of the
infinitesimal area
of the world, the resolution of the sensor
as a function of the point on the image plane at the center of the
infinitesimal area  is:
is:
| 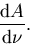 |
(29) |
Figure 8:
The geometry used to derive the spatial
resolution of a catadioptric sensor. Assuming the conventional
sensor has a frontal image plane which is located at a distance
u from the pinhole and the optical axis is aligned with the
z-axis  , the spatial resolution of
the conventional sensor is
, the spatial resolution of
the conventional sensor is  . Therefore the area of the mirror
imaged by the infinitesimal image plane area
. Therefore the area of the mirror
imaged by the infinitesimal image plane area  is
is
 . So, the solid angle of the world imaged
by the infinitesimal area
. So, the solid angle of the world imaged
by the infinitesimal area  on the image plane is
on the image plane is
 .Hence, the spatial resolution of the catadioptric sensor is
.Hence, the spatial resolution of the catadioptric sensor is
 since
since  .
.
 |
If  is the angle made between the optical axis and the line
joining the pinhole to the center of the infinitesimal area
is the angle made between the optical axis and the line
joining the pinhole to the center of the infinitesimal area
 (see Figure 8), the solid angle subtended
by the infinitesimal area
(see Figure 8), the solid angle subtended
by the infinitesimal area  at the pinhole is:
at the pinhole is:
| 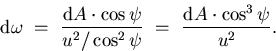 |
(30) |
Therefore, the resolution of the conventional camera is:
| 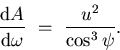 |
(31) |
Then, the area of the mirror imaged by the infinitesimal area
 is:
is:
|  |
(32) |
where  is the angle between the normal to the mirror at
(r,z) and the line joining the pinhole to the mirror point (r,z).
Since reflection at the mirror is specular, the solid angle of the
world imaged by the catadioptric camera is:
is the angle between the normal to the mirror at
(r,z) and the line joining the pinhole to the mirror point (r,z).
Since reflection at the mirror is specular, the solid angle of the
world imaged by the catadioptric camera is:
| 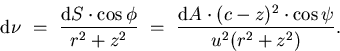 |
(33) |
Therefore, the resolution of the catadioptric camera is:
| ![\begin{displaymath}
\frac{\mathrm{d} A}{\mathrm{d} \nu} \ = \
\frac{u^{2} (r^{2}...
...psi }{(c-z)^{2}}\right]
\frac{\mathrm{d} A}{\mathrm{d} \omega}.\end{displaymath}](img99.gif) |
(34) |
But, since:
| 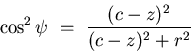 |
(35) |
we have:
| ![\begin{displaymath}
\frac{\mathrm{d} A}{\mathrm{d} \nu} \ = \
\left[\frac{r^{2}+...
...-z)^{2} + r^{2}}\right]
\frac{\mathrm{d} A}{\mathrm{d} \omega}.\end{displaymath}](img101.gif) |
(36) |
Hence, the resolution of the catadioptric camera is the resolution of
the conventional camera used to construct it multiplied by a factor of:
| 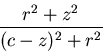 |
(37) |
where (r,z) is the point on the mirror being imaged.
The first thing to note from Equation (38) is that
for the planar mirror  , the resolution of the
catadioptric sensor is the same as that of the conventional
sensor used to construct it. This is as expected by symmetry.
Secondly, note that the factor in Equation (39) is the
square of the distance from the point (r,z) to the effective
viewpoint
, the resolution of the
catadioptric sensor is the same as that of the conventional
sensor used to construct it. This is as expected by symmetry.
Secondly, note that the factor in Equation (39) is the
square of the distance from the point (r,z) to the effective
viewpoint  , divided by the square of the distance to
the pinhole
, divided by the square of the distance to
the pinhole  . Let
. Let  denote the distance
from the viewpoint to (r,z) and
denote the distance
from the viewpoint to (r,z) and  the distance of (r,z)
from the pinhole. Then, the factor in Equation (39)
is
the distance of (r,z)
from the pinhole. Then, the factor in Equation (39)
is  For the ellipsoid,
For the ellipsoid,  for
some constant
for
some constant  . Therefore, for the ellispoid
the factor is:
. Therefore, for the ellispoid
the factor is:
|  |
(38) |
which increases as  decreases and
decreases and  increases.
For the hyperboloid,
increases.
For the hyperboloid,  for
some constant
for
some constant  . Therefore, for the
hyperboloid the factor is:
. Therefore, for the
hyperboloid the factor is:
| 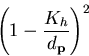 |
(39) |
which increases as  increases and
increases and  increases. So, for both ellipsoids and hyperboloids,
the factor in Equation (39) increases with r. Hence
both hyperboloidal and ellipsoidal catadioptric sensors constructed
with a uniform resolution conventional camera will have their highest
resolution around the periphery, a useful property for certain
applications such as teleconferencing.
increases. So, for both ellipsoids and hyperboloids,
the factor in Equation (39) increases with r. Hence
both hyperboloidal and ellipsoidal catadioptric sensors constructed
with a uniform resolution conventional camera will have their highest
resolution around the periphery, a useful property for certain
applications such as teleconferencing.



Next: Defocus Blur of a
Up: No Title
Previous: Hyperboloidal Mirrors
Simon Baker
1/22/1998

![]() is the angle made between the optical axis and the line
joining the pinhole to the center of the infinitesimal area
is the angle made between the optical axis and the line
joining the pinhole to the center of the infinitesimal area
![]() (see Figure 8), the solid angle subtended
by the infinitesimal area
(see Figure 8), the solid angle subtended
by the infinitesimal area ![]() at the pinhole is:
at the pinhole is:
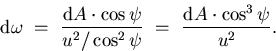
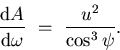

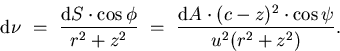
![\begin{displaymath}
\frac{\mathrm{d} A}{\mathrm{d} \nu} \ = \
\frac{u^{2} (r^{2}...
...psi }{(c-z)^{2}}\right]
\frac{\mathrm{d} A}{\mathrm{d} \omega}.\end{displaymath}](img99.gif)
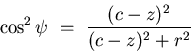
![\begin{displaymath}
\frac{\mathrm{d} A}{\mathrm{d} \nu} \ = \
\left[\frac{r^{2}+...
...-z)^{2} + r^{2}}\right]
\frac{\mathrm{d} A}{\mathrm{d} \omega}.\end{displaymath}](img101.gif)
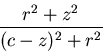
![]() , the resolution of the
catadioptric sensor is the same as that of the conventional
sensor used to construct it. This is as expected by symmetry.
Secondly, note that the factor in Equation (39) is the
square of the distance from the point (r,z) to the effective
viewpoint
, the resolution of the
catadioptric sensor is the same as that of the conventional
sensor used to construct it. This is as expected by symmetry.
Secondly, note that the factor in Equation (39) is the
square of the distance from the point (r,z) to the effective
viewpoint ![]() , divided by the square of the distance to
the pinhole
, divided by the square of the distance to
the pinhole ![]() . Let
. Let ![]() denote the distance
from the viewpoint to (r,z) and
denote the distance
from the viewpoint to (r,z) and ![]() the distance of (r,z)
from the pinhole. Then, the factor in Equation (39)
is
the distance of (r,z)
from the pinhole. Then, the factor in Equation (39)
is ![]() For the ellipsoid,
For the ellipsoid, ![]() for
some constant
for
some constant ![]() . Therefore, for the ellispoid
the factor is:
. Therefore, for the ellispoid
the factor is: