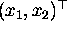 , while the homogeneous coordinates are a 3-vector
, while the homogeneous coordinates are a 3-vector 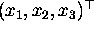 .
The simplest way to assign the third component is to make it
equal to one
.
The simplest way to assign the third component is to make it
equal to one ,
,



The equations for perspective projection to the image plane are non-linear when expressed in non-homogeneous coordinates, but are linear in homogeneous coordinates. This is characteristic of all transformations in projective geometry, not just perspective projection. It provides one of the main motivations for the use of homogeneous coordinates, since linear systems are symbolically and numerically easier to handle than non-linear ones.
The non-homogeneous coordinates of an image point are a 2-vector
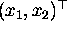 , while the homogeneous coordinates are a 3-vector
, while the homogeneous coordinates are a 3-vector 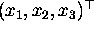 .
The simplest way to assign the third component is to make it
equal to one
.
The simplest way to assign the third component is to make it
equal to one ,
,
An important property of homogeneous coordinates is that a pair of homogeneous vectors are equivalent if one is a scalar multiple of the other,
where 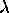 is a scalar,
is a scalar, 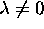 .
.
This equivalence is plain when one considers the transformation from homogeneous coordinates back to image plane coordinates, which is carried out by reversing the process for converting into homogeneous coordinates - scale the homogeneous vector such that the third component is equal to one and then discard the third component. For the homogeneous vector in Equation 1,
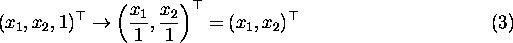
and for the equivalent homogeneous vector in Equation 2,
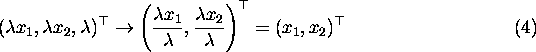
so all equivalent homogeneous coordinates correspond to the same non-homogeneous coordinates as expected.
Image lines are also represented by
3-vectors in homogeneous coordinates. The homogeneous points
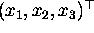 which lie on the homogeneous line
which lie on the homogeneous line
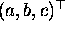 are specified by the equation,
are specified by the equation,
As was the case for points, homogeneous coordinates for lines are equivalent if one is a scalar multiple of the other.
In addition to the linearity which they bring to equations, a further
important benefit of using homogeneous coordinates is that they make it
possible to represent points which are at infinity on the image plane.
In non-homogeneous coordinates, there is no numerical representation
for a point at infinity; in homogeneous coordinates, such a
point has its third component equal to zero i.e. it has the form
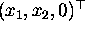 . Points at infinity are called ideal
points
. Points at infinity are called ideal
points .
The commonest way in which an ideal point arises in
practice is as the intersection point of two parallel lines.
Note that having obtained a representation for ideal points, there
is no need to treat them differently from any other point
on the image plane - the manipulations and transformations of
projective geometry apply equally well to all points both non-ideal
and ideal.
When the set of non-ideal and ideal points is taken together, the
result is called a projective plane.
.
The commonest way in which an ideal point arises in
practice is as the intersection point of two parallel lines.
Note that having obtained a representation for ideal points, there
is no need to treat them differently from any other point
on the image plane - the manipulations and transformations of
projective geometry apply equally well to all points both non-ideal
and ideal.
When the set of non-ideal and ideal points is taken together, the
result is called a projective plane.


