


Next: About this document
Up: Important concepts from projective
Previous: Projective Invariants
Ideal points on the projective plane are located at infinity, and have coordinates of the
form 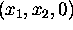 . There is just one free parameter in the coordinates of an
ideal point because the scale of a homogeneous vector is
arbitrary - thus the set of all ideal points on the projective plane
constitutes a line, called the ideal line. In the same way, the
ideal points of projective 3-space have the form
. There is just one free parameter in the coordinates of an
ideal point because the scale of a homogeneous vector is
arbitrary - thus the set of all ideal points on the projective plane
constitutes a line, called the ideal line. In the same way, the
ideal points of projective 3-space have the form 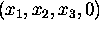 and
constitute
a plane called the ideal plane, and so on for projective spaces of any
dimension.
and
constitute
a plane called the ideal plane, and so on for projective spaces of any
dimension.
The image of an ideal point under a projectivity is
called a vanishing point, the image of an ideal line is called a
vanishing line, and so on. A familiar example
of the formation of a vanishing point is shown in Figure
4. A camera with focal point C views a scene in which
there are a pair of parallel lines M and N. Lines M and N
appear in the
image as converging lines m and n
which meet at the vanishing point V. An
important feature which is discussed below is that the line CV
is parallel to lines M and N.
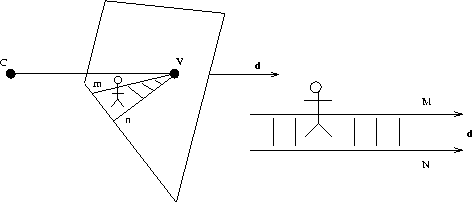
Figure:
The camera centre is at C. The parallel lines M and
N in the scene give rise to converging lines m and n
in the image which
meet at the vanishing point V. The line CV is parallel to
the lines M and N, with direction vector d.
An algebraic analysis of this configuration would describe the
following - lines M and N are parallel and so meet at
infinity at an ideal point; the image of M and N
meeting at the ideal point is m and n
meeting at the
vanishing point V (the image of the ideal point is V) -
note that concurrency is preserved under a
projective transformation, so concurrency at the ideal point in the
world is reflected in concurrency at V in the
image; finally, the ray CV must
itself be incident with the ideal point because this is perspective
projection, and hence the ray CV is parallel to
lines M and N in the scene.
The analysis would involve some complication, because
lines are more difficult to manipulate in projective 3-space than they
are on the projective plane. In fact, an algebraic analysis is
unnecessary to gain a reasonable understanding of the physical
configuration, which can be obtained instead by a straightforward
geometric argument as below.
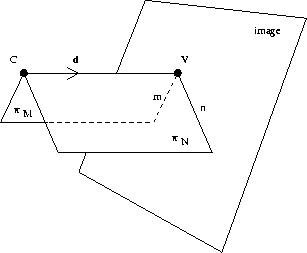
Figure:
Two planes constructed in the way described in the text. By the
arguments in the text, C and V are both on the line of
intersection of the two planes, and the line of intersection has
direction d (see Figure 4). Thus, CV is
parallel to the lines M and N in the scene in Figure 4.
Referring again to Figure 4, consider a plane 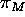 through C and line M, and a plane
through C and line M, and a plane  through C and
line N. We now show that the line of intersection of the two
planes has the same direction d as lines M and N in the
scene, and that CV coincides with the line of intersection of the
two planes i.e. the line CV is parallel to the lines in the scene.
See Figure 5.
through C and
line N. We now show that the line of intersection of the two
planes has the same direction d as lines M and N in the
scene, and that CV coincides with the line of intersection of the
two planes i.e. the line CV is parallel to the lines in the scene.
See Figure 5.
First note that the line of intersection
of 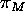 and
and 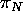 has direction
has direction 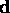 because both planes
because both planes 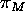 and
and 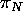 have
have 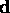 as a basis
vector. Now note that
as a basis
vector. Now note that 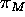 intersects the image plane along m,
and similarly
intersects the image plane along m,
and similarly 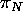 intersects the image plane along n. Thus,
the line of intersection of
intersects the image plane along n. Thus,
the line of intersection of 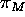 and
and  passes through the point of intersection of m and n which is the vanishing point V.
The line of intersection of
passes through the point of intersection of m and n which is the vanishing point V.
The line of intersection of 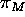 and
and 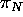 also passes
through C, because C is incident with both planes.
Thus, CV coincides with the line of intersection of
also passes
through C, because C is incident with both planes.
Thus, CV coincides with the line of intersection of 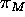 and
and
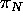 , and the argument is concluded.
, and the argument is concluded.
The discussion can be extended to the imaging of a plane, as shown in
Figure 6. A camera with focal point C views a
tiled plane 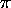 .
One set of parallel lines on
.
One set of parallel lines on  is concurrent at the ideal point
is concurrent at the ideal point
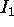 , and the other set is concurrent at
, and the other set is concurrent at 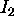 . The line through
. The line through
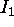 and
and 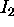 is the ideal line (the horizon) of the plane.
The image of
is the ideal line (the horizon) of the plane.
The image of 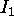 is the vanishing point
is the vanishing point 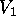 , the image of
, the image of 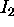 is
the vanishing point
is
the vanishing point 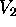 , and the image of the ideal line is the
vanishing line L.
An important feature of this configuration, which can
be demonstrated using similar arguments to those above, is that
the normal of the plane defined
by C and L is parallel to the normal of the
plane
, and the image of the ideal line is the
vanishing line L.
An important feature of this configuration, which can
be demonstrated using similar arguments to those above, is that
the normal of the plane defined
by C and L is parallel to the normal of the
plane 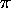 - see Figure 6b.
- see Figure 6b.
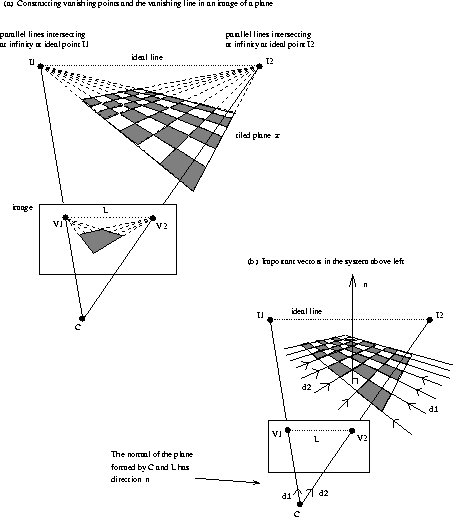
Figure:
(a) One set of parallel lines on the plane 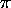 is concurrent at the ideal point
is concurrent at the ideal point
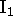 , and the other set is concurrent at
, and the other set is concurrent at 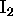 . The line through
. The line through
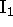 and
and  is the ideal line (the horizon) of the plane.
The image of
is the ideal line (the horizon) of the plane.
The image of 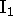 is the vanishing point
is the vanishing point 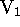 , the image of
, the image of  is
the vanishing point
is
the vanishing point  , and the image of the ideal line is the
vanishing line
, and the image of the ideal line is the
vanishing line 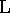 .
(b) Note that
the plane formed by
.
(b) Note that
the plane formed by  and L has the same normal as the plane
and L has the same normal as the plane 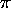 .
.



Next: About this document
Up: Important concepts from projective
Previous: Projective Invariants
Bob Fisher
Fri Nov 7 12:08:26 GMT 1997
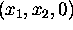 . There is just one free parameter in the coordinates of an
ideal point because the scale of a homogeneous vector is
arbitrary - thus the set of all ideal points on the projective plane
constitutes a line, called the ideal line. In the same way, the
ideal points of projective 3-space have the form
. There is just one free parameter in the coordinates of an
ideal point because the scale of a homogeneous vector is
arbitrary - thus the set of all ideal points on the projective plane
constitutes a line, called the ideal line. In the same way, the
ideal points of projective 3-space have the form 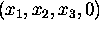 and
constitute
a plane called the ideal plane, and so on for projective spaces of any
dimension.
and
constitute
a plane called the ideal plane, and so on for projective spaces of any
dimension.





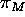 through C and line M, and a plane
through C and line M, and a plane  through C and
line N. We now show that the line of intersection of the two
planes has the same direction d as lines M and N in the
scene, and that CV coincides with the line of intersection of the
two planes i.e. the line CV is parallel to the lines in the scene.
See Figure
through C and
line N. We now show that the line of intersection of the two
planes has the same direction d as lines M and N in the
scene, and that CV coincides with the line of intersection of the
two planes i.e. the line CV is parallel to the lines in the scene.
See Figure 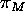 and
and 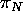 has direction
has direction 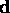 because both planes
because both planes 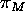 and
and 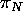 have
have 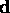 as a basis
vector. Now note that
as a basis
vector. Now note that 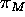 intersects the image plane along m,
and similarly
intersects the image plane along m,
and similarly 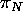 intersects the image plane along n. Thus,
the line of intersection of
intersects the image plane along n. Thus,
the line of intersection of 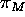 and
and  passes through the point of intersection of m and n which is the vanishing point V.
The line of intersection of
passes through the point of intersection of m and n which is the vanishing point V.
The line of intersection of 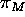 and
and 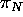 also passes
through C, because C is incident with both planes.
Thus, CV coincides with the line of intersection of
also passes
through C, because C is incident with both planes.
Thus, CV coincides with the line of intersection of 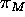 and
and
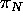 , and the argument is concluded.
, and the argument is concluded.
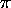 .
One set of parallel lines on
.
One set of parallel lines on  is concurrent at the ideal point
is concurrent at the ideal point
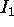 , and the other set is concurrent at
, and the other set is concurrent at 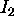 . The line through
. The line through
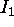 and
and 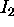 is the ideal line (the horizon) of the plane.
The image of
is the ideal line (the horizon) of the plane.
The image of 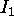 is the vanishing point
is the vanishing point 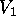 , the image of
, the image of 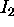 is
the vanishing point
is
the vanishing point 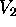 , and the image of the ideal line is the
vanishing line L.
An important feature of this configuration, which can
be demonstrated using similar arguments to those above, is that
the normal of the plane defined
by C and L is parallel to the normal of the
plane
, and the image of the ideal line is the
vanishing line L.
An important feature of this configuration, which can
be demonstrated using similar arguments to those above, is that
the normal of the plane defined
by C and L is parallel to the normal of the
plane 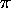 - see Figure
- see Figure 
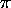 is concurrent at the ideal point
is concurrent at the ideal point
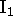 , and the other set is concurrent at
, and the other set is concurrent at 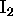 . The line through
. The line through
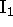 and
and  is the ideal line (the horizon) of the plane.
The image of
is the ideal line (the horizon) of the plane.
The image of 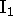 is the vanishing point
is the vanishing point 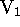 , the image of
, the image of  is
the vanishing point
is
the vanishing point  , and the image of the ideal line is the
vanishing line
, and the image of the ideal line is the
vanishing line 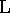 .
(b) Note that
the plane formed by
.
(b) Note that
the plane formed by  and L has the same normal as the plane
and L has the same normal as the plane 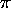 .
.