



Next: Multi-Dimensional Search
Up: Minimization in One
Previous: Minimization in One
An elegant and robust method of locating a minimum in such a bracket is
the Golden Section Search. This involves evaluating the function at some
point x in the larger of the two intervals 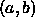 or
or 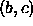 . If
. If 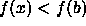 then x replaces the midpoint b, and b becomes an end point. If
then x replaces the midpoint b, and b becomes an end point. If 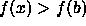 then
b remains the midpoint with x replacing one of the end points. Either way
the width of the bracketing interval will reduce and the position of the minima
will be better defined (Figure 2). The procedure is then repeated until the width achieves
a desired tolerance. It can be shown that if the new test point, x, is
chosen to be a proportion
then
b remains the midpoint with x replacing one of the end points. Either way
the width of the bracketing interval will reduce and the position of the minima
will be better defined (Figure 2). The procedure is then repeated until the width achieves
a desired tolerance. It can be shown that if the new test point, x, is
chosen to be a proportion 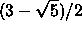 (hence Golden Section) along the larger sub-interval,
measured from the mid-point b, then the width of the full interval
(hence Golden Section) along the larger sub-interval,
measured from the mid-point b, then the width of the full interval 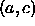 will reduce at an optimal rate [6].
will reduce at an optimal rate [6].
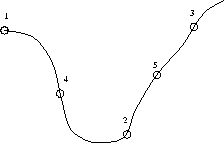
Figure 2: Golden Section Search. Initial bracket (1,2,3) becomes (4,2,3), (4,2,5)...
The Golden Section Search requires no information about the derivative
of the function. If such information is available it can be used to
predict where best to choose the new point x in the above algorithm, leading
to faster convergence
[6].
Bob Fisher
Fri Mar 28 14:12:50 GMT 1997
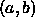 or
or 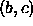 . If
. If 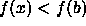 then x replaces the midpoint b, and b becomes an end point. If
then x replaces the midpoint b, and b becomes an end point. If 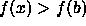 then
b remains the midpoint with x replacing one of the end points. Either way
the width of the bracketing interval will reduce and the position of the minima
will be better defined (Figure 2). The procedure is then repeated until the width achieves
a desired tolerance. It can be shown that if the new test point, x, is
chosen to be a proportion
then
b remains the midpoint with x replacing one of the end points. Either way
the width of the bracketing interval will reduce and the position of the minima
will be better defined (Figure 2). The procedure is then repeated until the width achieves
a desired tolerance. It can be shown that if the new test point, x, is
chosen to be a proportion 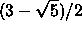 (hence Golden Section) along the larger sub-interval,
measured from the mid-point b, then the width of the full interval
(hence Golden Section) along the larger sub-interval,
measured from the mid-point b, then the width of the full interval 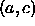 will reduce at an optimal rate [6].
will reduce at an optimal rate [6].




